Velocity inertial subrange model: Difference between revisions
| (52 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{DefineConcept | {{DefineConcept | ||
|description=The inertial subrange separates the energy-containing production range from the viscous dissipation range. | |description=The inertial subrange separates the energy-containing production range from the viscous dissipation range. | ||
|article_type= | |article_type=Fundamentals | ||
|instrument_type=Velocity point-measurements, Velocity profilers | |instrument_type=Velocity point-measurements, Velocity profilers | ||
}} | }} | ||
== | == Model for steady-flows == | ||
This theoretical model predicts the spectral shape of velocities in wavenumber space. | This theoretical model predicts the spectral shape of velocities in wavenumber space. | ||
<math>\ | <math>\Psi_{Vj}(\hat{k})=a_jC_k\varepsilon^{2/3}\hat{k}^{-5/3}</math> | ||
[[File:InertialSubrangeSchematic.png|thumb|Sketch of velocity power density spectrum in log-log space. The inertial subrange's -5/3 slope is highlighted. The vertical axis represents <math>\Psi_{Vj}(\hat{k})</math>. Large scale [[#anisotropy|turbulence anisotropy]] in low energy flow may alter the expected spectral shape]] | |||
Here <math>\hat{k}</math> is expressed in rad/m and <math>Vj</math> represents the velocities <math>V</math> in direction <math>j</math>. <math>C_k</math> is the empirical Kolmogorov universal constant of C | Here <math>\hat{k}</math> is expressed in rad/m and <math>Vj</math> represents the velocities <math>V</math> in direction <math>j</math>. <math>C_k</math> is the empirical Kolmogorov universal constant of C | ||
= 1.5 | = 1.5 <ref name="Sreenivasan">{{Cite journal | ||
|authors= K. R. Sreenivasan | |||
|journal_or_publisher= Phys. Fluids | |||
|paper_or_booktitle= On the universality of the Kolmogorov constant | |||
|year= 1995 | |||
|doi= 10.1063/1.868656 | |||
}}</ref>. Amongst the three direction, the spectra deviates by the constant <math>a_j</math>: | |||
<ref name="Pope">{{Cite journal | |||
|authors= S.B Pope | |||
|journal_or_publisher= Cambridge Univ. Press | |||
|paper_or_booktitle= Turbulent flows | |||
|year= 2000 | |||
|doi= 10.1017/CBO9780511840531 | |||
}}</ref> | |||
* In the longitudinal direction, i.e., the direction of mean advection (j=1), <math>a_1=\frac{18}{55}</math> | * In the longitudinal direction, i.e., the direction of mean advection (j=1), <math>a_1=\frac{18}{55}</math> | ||
* In the other directions <math>a_2=a_3=\frac{4}{3}a_1</math> | * In the other directions <math>a_2=a_3=\frac{4}{3}a_1</math> | ||
== Models influenced by surface waves == | |||
{{FontColor|fg=white|bg=red|text=Need to add equations and figures from Lumley & Terray}}<ref name="Lumley_Terray"> | |||
{{Cite journal | |||
|authors=J. Lumley and E. Terray | |||
|journal_or_publisher=J. Phys. Oceanogr | |||
|paper_or_booktitle=Kinematics of turbulence convected by a random wave field | |||
|year=1983 | |||
|doi= 10.1175/1520-0485(1983)<2000:KOTCBA>2.0.CO;2 | |||
}} | |||
</ref> | |||
== Inertial subrange collapse and <span id="anisotropy">anisotropy</span> == | |||
Near boundaries or low energy environments--defined as flows with a small separation between the large turbulent overturns <math>L</math> and the smallest (Kolmogorov)-- tends to adversely impact our ability to estimate <math>\varepsilon</math> from the lower wavenumbers. In certain cases, the velocity spectra may not have a sufficiently developed inertial subrange to estimate <math>\varepsilon</math> <ref name="Gargett.etal1984">{{Cite journal | |||
|authors= A. E. Gargett, T. R. Osborn, and P.W. Nasmyth | |||
|journal_or_publisher= J. Fluid. Mech. | |||
|paper_or_booktitle= Local isotropy and the decay of turbulence in a stratified fluid | |||
|year= 1984 | |||
|doi=10.1017/S0022112084001592 | |||
}}</ref><ref name="Bluteau.etal2011">{{Cite journal | |||
|authors= C.E. Bluteau, N.L. Jones, and G. Ivey | |||
|journal_or_publisher= Limnol. Oceanogr.: Methods | |||
|paper_or_booktitle= Estimating turbulent kinetic energy dissipation using the inertial subrange method in environmental flows | |||
|year= 2011 | |||
|doi=10:4319/lom.2011.9.302 | |||
}}</ref>. | |||
[[Velocity inertial subrange model#anisotropy|Anisotropic velocity spectra]] are exhibited when the largest turbulence scales are less than {{FontColor|fg=white|bg=red|text=XX}} times the Kolmogorov length scale, may inhibit using the vertical velocity component to derive <math>\varepsilon</math>. In these situations, it may be possible to use the longitudinal velocity component (see Bluteau et al. 2011<ref name="Bluteau.etal2011"/>), which requires the user to [[Rotation of the velocity measurements|rotate the velocity]] in the direction of the mean flow. | |||
[[File: | [[File:Anisotropy.png|center|thumbnail|600px|Example of how [[Velocity inertial subrange model#anisotropy| turbulence anisotropy]] influences the velocity spectral shapes. This instrument was located very close to the bed (0.15 m) in a shallow waterway less than 2 m deep, which results in the vertical velocity's inertial subrange being reduced by the flattening of the spectra at wavenumbers of 10 cpm (0.1m scales). Strong stratification (or shear) is another mechanism that shortens the inertial subrange at the lower wavenumbers<ref name="Bluteau.etal2011"/>. The wavenumber at which its impact is felt is approximately <math>L_o/3</math> where <math>L_o</math> is the Ozmidov length scale.]] | ||
== | == Notes == | ||
Latest revision as of 18:54, 5 July 2022
| Short definition of Velocity inertial subrange model |
|---|
| The inertial subrange separates the energy-containing production range from the viscous dissipation range. |
This is the common definition for Velocity inertial subrange model, but other definitions maybe discussed within the wiki.
Model for steady-flows
This theoretical model predicts the spectral shape of velocities in wavenumber space.
[math]\displaystyle{ \Psi_{Vj}(\hat{k})=a_jC_k\varepsilon^{2/3}\hat{k}^{-5/3} }[/math]

Here [math]\displaystyle{ \hat{k} }[/math] is expressed in rad/m and [math]\displaystyle{ Vj }[/math] represents the velocities [math]\displaystyle{ V }[/math] in direction [math]\displaystyle{ j }[/math]. [math]\displaystyle{ C_k }[/math] is the empirical Kolmogorov universal constant of C = 1.5 [1]. Amongst the three direction, the spectra deviates by the constant [math]\displaystyle{ a_j }[/math]: [2]
- In the longitudinal direction, i.e., the direction of mean advection (j=1), [math]\displaystyle{ a_1=\frac{18}{55} }[/math]
- In the other directions [math]\displaystyle{ a_2=a_3=\frac{4}{3}a_1 }[/math]
Models influenced by surface waves
Need to add equations and figures from Lumley & Terray[3]
Inertial subrange collapse and anisotropy
Near boundaries or low energy environments--defined as flows with a small separation between the large turbulent overturns [math]\displaystyle{ L }[/math] and the smallest (Kolmogorov)-- tends to adversely impact our ability to estimate [math]\displaystyle{ \varepsilon }[/math] from the lower wavenumbers. In certain cases, the velocity spectra may not have a sufficiently developed inertial subrange to estimate [math]\displaystyle{ \varepsilon }[/math] [4][5].
Anisotropic velocity spectra are exhibited when the largest turbulence scales are less than XX times the Kolmogorov length scale, may inhibit using the vertical velocity component to derive [math]\displaystyle{ \varepsilon }[/math]. In these situations, it may be possible to use the longitudinal velocity component (see Bluteau et al. 2011[5]), which requires the user to rotate the velocity in the direction of the mean flow.
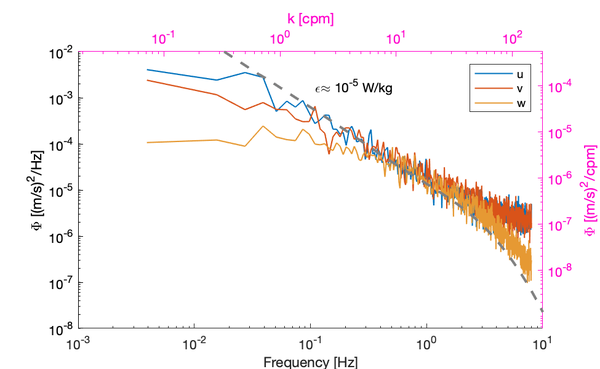
Notes
- ↑ K. R. Sreenivasan. 1995. On the universality of the Kolmogorov constant. Phys. Fluids. doi:10.1063/1.868656
- ↑ S.B Pope. 2000. Turbulent flows. Cambridge Univ. Press. doi:10.1017/CBO9780511840531
- ↑ J. Lumley and E. Terray. 1983. Kinematics of turbulence convected by a random wave field. J. Phys. Oceanogr. doi:<2000:KOTCBA>2.0.CO;2 10.1175/1520-0485(1983)<2000:KOTCBA>2.0.CO;2
- ↑ A. E. Gargett, T. R. Osborn and and P.W. Nasmyth. 1984. Local isotropy and the decay of turbulence in a stratified fluid. J. Fluid. Mech.. doi:10.1017/S0022112084001592
- ↑ 5.0 5.1 5.2 C.E. Bluteau, N.L. Jones and and G. Ivey. 2011. Estimating turbulent kinetic energy dissipation using the inertial subrange method in environmental flows. Limnol. Oceanogr.: Methods. doi:10:4319/lom.2011.9.302
