Example forward-difference: Difference between revisions
No edit summary |
No edit summary |
||
| Line 7: | Line 7: | ||
The square of the velocity difference between bins separated by <math>\delta</math> bins is then evaluated for each <math>t</math>. So for <math>t_1</math>, bin 1 and <math>\delta=1</math>, we get: | The square of the velocity difference between bins separated by <math>\delta</math> bins is then evaluated for each <math>t</math>. So for <math>t_1</math>, bin 1 and <math>\delta=1</math>, we get: | ||
:<math>\Delta{v}(1,1,1) = \left[v^\prime(1,1) - v^\prime(2,1)\right]^2</math> | :<math>\Delta{v^\prime}(1,1,1) = \left[v^\prime(1,1) - v^\prime(2,1)\right]^2</math> | ||
For bin 1 the squared velocity difference can be evaluated for <math>1\leqslant\delta\leqslant29</math>, whilst for bin 2 it is restricted to <math>1\leqslant\delta\leqslant28</math>, reducing by 1 with each bin, so that for bin 29, it can only be evaluated for <math>\delta=1</math> and there are no options for bin 30. This is summarised as follows: | For bin 1 the squared velocity difference can be evaluated for <math>1\leqslant\delta\leqslant29</math>, whilst for bin 2 it is restricted to <math>1\leqslant\delta\leqslant28</math>, reducing by 1 with each bin, so that for bin 29, it can only be evaluated for <math>\delta=1</math> and there are no options for bin 30. This is summarised as follows: | ||
Revision as of 17:35, 12 November 2021
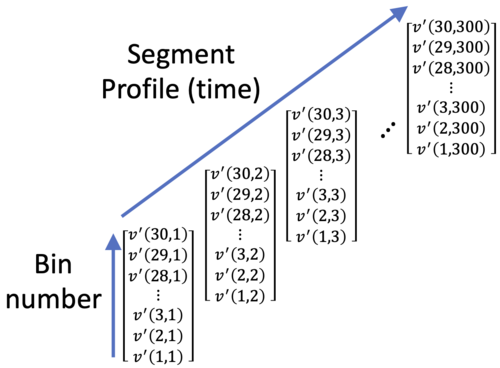
Consider the example of an ADCP with a beam angle of <math>20^{\circ}</math>, configured with a vertical bin size of 10 cm, recording profiles at 1 second intervals with a data segment length of 300 seconds. The Level 1 QC of the data identified that good data was typically returned from bins 1 to 30.
The velocity data from a single beam for a single data segment can therefore be visualised as:
The square of the velocity difference between bins separated by <math>\delta</math> bins is then evaluated for each <math>t</math>. So for <math>t_1</math>, bin 1 and <math>\delta=1</math>, we get:
- <math>\Delta{v^\prime}(1,1,1) = \left[v^\prime(1,1) - v^\prime(2,1)\right]^2</math>
For bin 1 the squared velocity difference can be evaluated for <math>1\leqslant\delta\leqslant29</math>, whilst for bin 2 it is restricted to <math>1\leqslant\delta\leqslant28</math>, reducing by 1 with each bin, so that for bin 29, it can only be evaluated for <math>\delta=1</math> and there are no options for bin 30. This is summarised as follows:

The mean is then taken across the 300 profiles in the data segment e.g.
- <math>D(1,1) = \sum_{t=1}^{300}D(1,\delta,t)</math>
Return to Forward-difference
