Rotation of the velocity measurements: Difference between revisions
mNo edit summary |
mNo edit summary |
||
| Line 3: | Line 3: | ||
|level=level 2 segmented and quality controlled | |level=level 2 segmented and quality controlled | ||
}} | }} | ||
==Velocity measurement frame== | ==Velocity measurement frame== | ||
The velocities are measured in either the instrument's coordinate system (XYZ), beam coordinates, or more rarely in the earth's coordinate system (ENU=east, north, and up). When estimating <math>\varepsilon</math>, measured velocities are often rotated in the flow's frame of reference since [[Velocity inertial subrange model|inertial subrange model]] differs between the velocity components, and the effects of [[Anisotropic turbulence|anisotropy]] are more pronounced in the transverse and vertical direction. When the vertical velocities are too heavily impacted by [[Anisotropic turbulence|anisotropy]], the longitudinal direction may be used to derive <math>\varepsilon</math>. In these instances, the longitudinal velocity must align with the mean flow direction, which may require rotating the measurements into a new frame of reference i.e., the analysis frame of reference. | The velocities are measured in either the instrument's coordinate system (XYZ), beam coordinates, or more rarely in the earth's coordinate system (ENU=east, north, and up). When estimating <math>\varepsilon</math>, measured velocities are often rotated in the flow's frame of reference since [[Velocity inertial subrange model|inertial subrange model]] differs between the velocity components, and the effects of [[Anisotropic turbulence|anisotropy]] are more pronounced in the transverse and vertical direction. When the vertical velocities are too heavily impacted by [[Anisotropic turbulence|anisotropy]], the longitudinal direction may be used to derive <math>\varepsilon</math>. In these instances, the longitudinal velocity must align with the mean flow direction, which may require rotating the measurements into a new frame of reference i.e., the analysis frame of reference. | ||
Revision as of 15:48, 2 June 2022
{{#default_form:Processing}}
{{#arraymap:
Velocity point-measurements
|,|x||}}
{{#arraymap:level 2 segmented and quality controlled|,|x||}}
Velocity measurement frame
The velocities are measured in either the instrument's coordinate system (XYZ), beam coordinates, or more rarely in the earth's coordinate system (ENU=east, north, and up). When estimating <math>\varepsilon</math>, measured velocities are often rotated in the flow's frame of reference since inertial subrange model differs between the velocity components, and the effects of anisotropy are more pronounced in the transverse and vertical direction. When the vertical velocities are too heavily impacted by anisotropy, the longitudinal direction may be used to derive <math>\varepsilon</math>. In these instances, the longitudinal velocity must align with the mean flow direction, which may require rotating the measurements into a new frame of reference i.e., the analysis frame of reference.
<be>
Analysis frame of reference
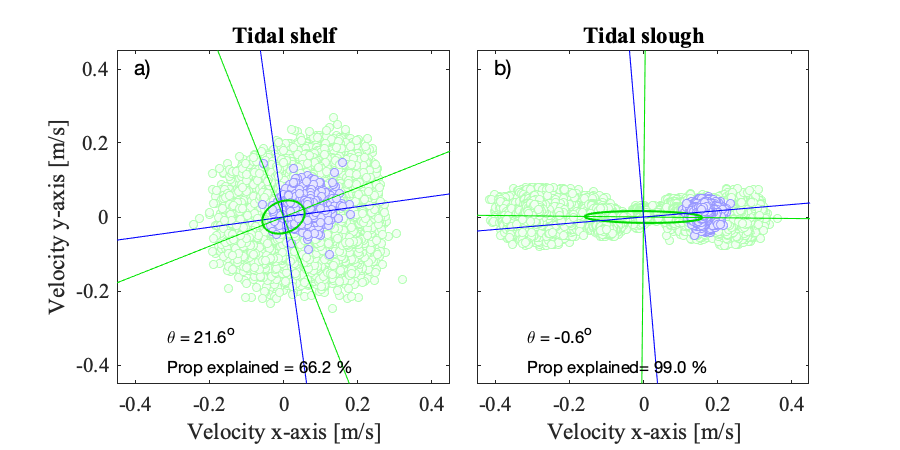
In some setups, the instrument's x-axis is already aligned with the general direction of the mean flow. This is particularly desirable when planning on calculating turbulent shear stresses via covariances as correlated noise may ensue when rotating the measurements into a new frame of reference (Insert reference). For some shallow systems, it's possible to align an instrument's x-axis with the direction of the flow (see Fig 1b). In these situations, the analysis frame of reference is the same as the instruments.
Alternatively, the entire dataset may be rotated using the velocities' principal components over the entire timeseries. For instance, the Tidal Slough example (Fig 1a) flows generally along the channel's length except at the turn of the tide. Using the same frame of reference throughout most of the dataset is acceptable. However, for other datasets such as the Tidal Shelf example, it's necessary to rotate each segment into the flow's direction.
Methods used for rotating into the analysis frame of reference
We will update when our final recommendation is set in stone. Also comment about large vertical velocities on sloped bottoms...
- Using time-averaged velocities in each segment
- Principal component analysis
