Velocity inertial subrange model: Difference between revisions
From Atomix
| Line 42: | Line 42: | ||
== Inertial subrange collapse and <span id="anisotropy">anisotropy</span> == | == Inertial subrange collapse and <span id="anisotropy">anisotropy</span> == | ||
Near boundaries or low energy environments | Near boundaries or low energy environments--defined as flows with a small separation between the large turbulent overturns <math>L</math> and the smallest (Kolmogorov)-- tends to adversely impact our ability to estimate <math>\varepsilon</math> from the lower wavenumbers. In certain cases, the velocity spectra may not have a sufficiently developed inertial subrange to estimate <math>\varepsilon</math> <ref name="Gargett.etal1984">{{Cite journal | ||
|authors= A. E. Gargett, T. R. Osborn, and P.W. Nasmyth | |||
|journal_or_publisher= J. Fluid. Mech. | |||
|paper_or_booktitle= Local isotropy and the decay of turbulence in a stratified fluid | |||
|year= 1984 | |||
|doi=10.1017/S0022112084001592 | |||
}}</ref><ref name="Bluteau.etal2011">{{Cite journal | |||
|authors= C.E. Bluteau, N.L. Jones, and G. Ivey | |authors= C.E. Bluteau, N.L. Jones, and G. Ivey | ||
|journal_or_publisher= Limnol. Oceanogr.: Methods | |journal_or_publisher= Limnol. Oceanogr.: Methods | ||
| Line 50: | Line 54: | ||
|year= 2011 | |year= 2011 | ||
|doi=10:4319/lom.2011.9.302 | |doi=10:4319/lom.2011.9.302 | ||
}}</ref>. The wavenumber at which its impact is felt is approximately <math>L_o/3</math> where <math>L_o</math> is the Ozmidov length scale.]] | }}</ref>. | ||
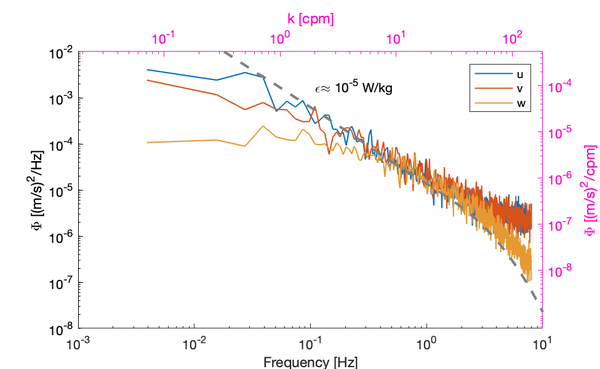
[[File:Anisotropy.png|center|thumbnail|600px|Example of how [[Velocity inertial subrange model#anisotropy| turbulence anisotropy]] influences the velocity spectral shapes. This instrument was located very close to the bed (0.15 m) in a shallow waterway less than 2 m deep, which results in the vertical velocity's inertial subrange being reduced by the flattening of the spectra at wavenumbers of 10 cpm (0.1m scales). Strong stratification (or shear) is another mechanism that shortens the inertial subrange at the lower wavenumbers<ref name="Bluteau.etal2011"/>. The wavenumber at which its impact is felt is approximately <math>L_o/3</math> where <math>L_o</math> is the Ozmidov length scale.]] | |||
== Notes == | == Notes == | ||
Revision as of 18:32, 5 July 2022
| Short definition of Velocity inertial subrange model |
|---|
| The inertial subrange separates the energy-containing production range from the viscous dissipation range. |
This is the common definition for Velocity inertial subrange model, but other definitions maybe discussed within the wiki.
Model for steady-flows
This theoretical model predicts the spectral shape of velocities in wavenumber space.
[math]\displaystyle{ \Psi_{Vj}(\hat{k})=a_jC_k\varepsilon^{2/3}\hat{k}^{-5/3} }[/math]
Here [math]\displaystyle{ \hat{k} }[/math] is expressed in rad/m and [math]\displaystyle{ Vj }[/math] represents the velocities [math]\displaystyle{ V }[/math] in direction [math]\displaystyle{ j }[/math]. [math]\displaystyle{ C_k }[/math] is the empirical Kolmogorov universal constant of C = 1.5 [1]. Amongst the three direction, the spectra deviates by the constant [math]\displaystyle{ a_j }[/math]: [2]
- In the longitudinal direction, i.e., the direction of mean advection (j=1), [math]\displaystyle{ a_1=\frac{18}{55} }[/math]
- In the other directions [math]\displaystyle{ a_2=a_3=\frac{4}{3}a_1 }[/math]
Models influenced by surface waves
Need to add equations and figures from Lumley & Terray[3]
Inertial subrange collapse and anisotropy
Near boundaries or low energy environments--defined as flows with a small separation between the large turbulent overturns [math]\displaystyle{ L }[/math] and the smallest (Kolmogorov)-- tends to adversely impact our ability to estimate [math]\displaystyle{ \varepsilon }[/math] from the lower wavenumbers. In certain cases, the velocity spectra may not have a sufficiently developed inertial subrange to estimate [math]\displaystyle{ \varepsilon }[/math] [4][5].
Notes
- ↑ K. R. Sreenivasan. 1995. On the universality of the Kolmogorov constant. Phys. Fluids. doi:10.1063/1.868656
- ↑ S.B Pope. 2000. Turbulent flows. Cambridge Univ. Press. doi:10.1017/CBO9780511840531
- ↑ J. Lumley and E. Terray. 1983. Kinematics of turbulence convected by a random wave field. J. Phys. Oceanogr. doi:<2000:KOTCBA>2.0.CO;2 10.1175/1520-0485(1983)<2000:KOTCBA>2.0.CO;2
- ↑ A. E. Gargett, T. R. Osborn and and P.W. Nasmyth. 1984. Local isotropy and the decay of turbulence in a stratified fluid. J. Fluid. Mech.. doi:10.1017/S0022112084001592
- ↑ 5.0 5.1 C.E. Bluteau, N.L. Jones and and G. Ivey. 2011. Estimating turbulent kinetic energy dissipation using the inertial subrange method in environmental flows. Limnol. Oceanogr.: Methods. doi:10:4319/lom.2011.9.302
