Velocity inertial subrange model

Short definition of Velocity inertial subrange model
The inertial subrange separates the energy-containing production range from the viscous dissipation range.

This is the common definition for Velocity inertial subrange model, but other definitions maybe discussed within the wiki.

{{#default_form:DefineConcept}} {{#arraymap:Velocity point-measurements, Velocity profilers|,|x||}}

Model for steady-flows

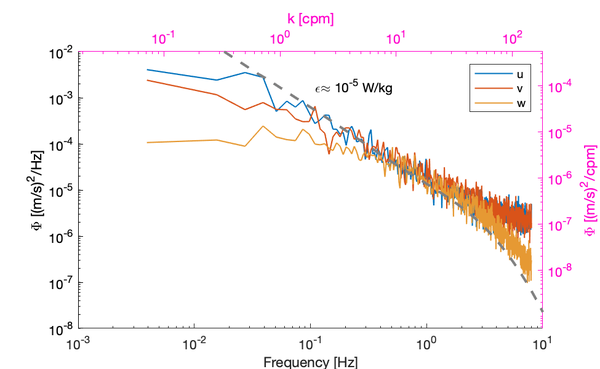
This theoretical model predicts the spectral shape of velocities in wavenumber space.

${\mathrm{\Psi }}_{Vj}(\hat{k})=a_j{C}_k{\epsilon }^{2/3}{\hat{k}}^{-5/3}$

Sketch of velocity power density spectrum in log-log space. The inertial subrange's -5/3 slope is highlighted. The vertical axis represents ${\mathrm{\Psi }}_{Vj}(\hat{k})$. Large scale turbulence anisotropy in low energy flow may alter the expected spectral shape

Here $\hat{k}$ is expressed in rad/m and $Vj$ represents the velocities $V$ in direction $j$. $C_k$ is the empirical Kolmogorov universal constant of C = 1.5 . Amongst the three direction, the spectra deviates by the constant $a_j$:

• In the longitudinal direction, i.e., the direction of mean advection (j=1), $a_1=\frac{18}{55}$
• In the other directions $a_2=a_3=\frac{4}{3}{a}_1$

Models influenced by surface waves

Need to add equations and figures from Lumley & Terray

Inertial subrange collapse and anisotropy

Near boundaries or low energy environments--defined as flows with a small separation between the large turbulent overturns $L$ and the smallest (Kolmogorov)-- tends to adversely impact our ability to estimate $\epsilon$ from the lower wavenumbers. In certain cases, the velocity spectra may not have a sufficiently developed inertial subrange to estimate $\epsilon$ .

Anisotropic velocity spectra are exhibited when the largest turbulence scales are less than XX times the Kolmogorov length scale, may inhibit using the vertical velocity component to derive $\epsilon$. In these situations, it may be possible to use the longitudinal velocity component (see Bluteau et al (2011)), which requires the user to rotate the velocity in the direction of the mean flow.

Example of how turbulence anisotropy influences the velocity spectral shapes. This instrument was located very close to the bed (0.15 m) in a shallow waterway less than 2 m deep, which results in the vertical velocity's inertial subrange being reduced by the flattening of the spectra at wavenumbers of 10 cpm (0.1m scales). Strong stratification (or shear) is another mechanism that shortens the inertial subrange at the lower wavenumbers. The wavenumber at which its impact is felt is approximately $L_o/3$ where $L_o$ is the Ozmidov length scale.