Spectra in the inertial subrange
| Short definition of Spectra in the inertial subrange |
|---|
| In the inertial subrange, the three-dimensional velocity spectrum follows a power-law behaviour and this makes it possible to easily derive the one-dimensional spectra, in this range |
This is the common definition for Spectra in the inertial subrange, but other definitions maybe discussed within the wiki.
In the inertial subrange, the three-dimensional velocity spectrum follows a power-law behaviour and this makes it possible to easily derive the one-dimensional spectra, in this range. Using ( ?) within the inertial subrange gives
[math]\displaystyle{ \tilde{F}_{11} (\hat{\kappa}_1) = \int_{\hat{\kappa}_1}^{\infty} \frac{F(\hat{\kappa})}{\hat{\kappa}} \left(1 - \frac{\hat{\kappa}_1^2}{\hat{\kappa}^2} \right)\, \mathrm{d}\hat{\kappa} = \frac{18}{55} C \hat{\kappa}_1^{-5/3} = C_1 \hat{\kappa}_1^{-5/3} }[/math]
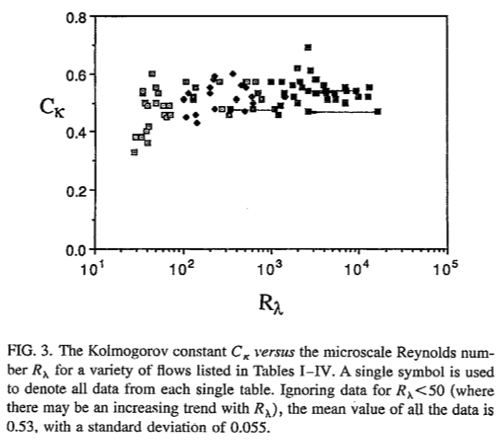
where [math]\displaystyle{ C_1=18C/55\approx27/55 }[/math] is frequently called the one-dimensional Kolmogorov constant, and the tilde is used to indicate these equations apply only in the inertial subrange. It is not possible to measure the three-dimensional spectrum and, thus, it is not possible to estimate [math]\displaystyle{ C }[/math] directly. Consequently, there is research interest in estimating </math>C_1</math> because it is the only practical way to determine the three-dimensional Kolmogorov constant [math]\displaystyle{ C }[/math]. Sreenivasa (1995)[1] compiled the values of the one-dimensional Kolmogorov constant reported from a wide range of measurements in the atmosphere, ocean, wind tunnels and pipes. The mean value (excluding low Reynolds number measurements) is [math]\displaystyle{ 0.53 }[/math] and the standard deviation is [math]\displaystyle{ 0.055 }[/math] (Figure 1). A crude estimate of the [math]\displaystyle{ 95\% }[/math] confidence interval is [math]\displaystyle{ C_1=0.53\pm0.03 }[/math].
Using [math]\displaystyle{ \tilde{F}_{22}= \frac{4}{3} \tilde{F}_{11} }[/math], the one-dimensional spectrum for the velocity components that are orthogonal to the direction of profiling is
[math]\displaystyle{ \tilde{F}_{22} (\hat{\kappa}_1) = \frac{4}{3} C_1 \hat{\kappa}_1^{-5/3} }[/math]
The gradient spectra in the inertial subrange are
[math]\displaystyle{ \begin{equation} \tilde{G}_{11} (\hat{\kappa}_1) = C_1 \hat{\kappa}_1^{1/3} \end{equation} }[/math]
and
[math]\displaystyle{ \begin{equation} \tilde{G}_{22} (\hat{\kappa}_1) = \frac{4}{3} C_1 \hat{\kappa}_1^{1/3} \end{equation} }[/math]
You want more? Go to Spectral integration