User talk:Rolf

Copied over the Here page into Rolf's discussion page. Users can use these pages for drafts/sandbox and notes. CynthiaBluteau (talk) 01:34, 14 December 2021 (CET)

The spectrum of Shear

This section provides a background on the spectrum of turbulence shear. We ask the user to refer to the many good references.

Spectra of velocity

The spectrum of velocity fluctuations has only been derived theoretically for the inertial subrange. This is the range of eddy sizes at which the flow is isotropic – they have lost the orientation of the largest eddies – but, their size is still large enough to not be significantly affected by viscosity. In this range kinetic energy is transferred to smaller scales through inertial interaction of the eddies but no energy is lost through friction. The three-dimensional spectrum of velocity, in the inertial subrange, is

[math]\displaystyle{ E(\kappa)=C\varepsilon^{2/3} \kappa^{-5/3} }[/math]

where [math]\displaystyle{ \kappa }[/math] is the magnitude of the angular wavenumber in units of [math]\displaystyle{ \mathrm{rad\,m^{-1}} }[/math] and [math]\displaystyle{ C\approx1.5 }[/math] is the three-dimensional Kolmogorov constant. There is no theoretical derivation for the velocity spectrum at wavenumbers beyond the inertial subrange. It is common to express the entire spectrum by

[math]\displaystyle{ E(\kappa)=C\varepsilon^{2/3} \kappa^{-5/3} f_{\eta} \left(\kappa_{L_K}\right) }[/math]

where [math]\displaystyle{ f_{\eta} }[/math] characterizes the spectrum in the dissipation range, has a value of unity in the inertial subrange ([math]\displaystyle{ \kappa L_K \ll 1 }[/math]), and [math]\displaystyle{ L_K=\left(\nu^3/\varepsilon\right)^{1/4} }[/math] is the Kolmogorov length. It is thought that the velocity spectrum can be described by a universal non-dimensional spectrum, [math]\displaystyle{ F }[/math], defined by

[math]\displaystyle{ E(\kappa) = \left(\varepsilon \nu^5 \right)^{1/4} F(\hat{\kappa}) }[/math]

where [math]\displaystyle{ \hat{\kappa} =\kappa L_K }[/math] is the non-dimensional wavenumber.

It is currently not possible to measure the three-dimensional spectrum of velocity. It is only possible to measure the one-dimensional spectrum of velocity – the spectrum derived from a profile in a single direction. The one-dimensional spectrum of the component of velocity that is parallel to the direction of profiling is

[math]\displaystyle{ E_{11} (\kappa_1 )= \int_{\kappa_1}^{\infty} \frac{E(\kappa)}{\kappa} \left( 1- \frac{\kappa_1^2}{\kappa^2} \right) \, \mathrm{d} \kappa }[/math]

where [math]\displaystyle{ \kappa_1 }[/math] is the angular wavenumber in the direction of profiling. The universal spectrum associated with [math]\displaystyle{ E_{11} }[/math] is given by

[math]\displaystyle{ E_{11} (\kappa_1) = \left( \varepsilon \nu^5 \right)^{1/4} F_{11} (\hat{\kappa}_1) }[/math]

and, therefore,

[math]\displaystyle{ F_{11} (\hat{\kappa}_1 )= \int_{\hat{\kappa}_1}^{\infty} \frac{F(\hat{\kappa})}{\hat{\kappa}} \left( 1- \frac{\hat{\kappa}_1^2}{\hat{\kappa}^2} \right) \, \mathrm{d} \hat{\kappa} }[/math]

Similarly, the one-dimensional spectrum of the component of velocity that is orthogonal to the direction of profiling is

[math]\displaystyle{ E_{22} (\kappa_1 ) = \frac{1}{2} \int_{\kappa_1}^{\infty} \frac{E(\kappa)}{\kappa} \left( 1 + \frac{\kappa_1^2}{\kappa^2} \right) \, \mathrm{d} \kappa }[/math]

and its universal spectrum is defined by

[math]\displaystyle{ E_{22} (\kappa_1) = \left(\varepsilon\nu^5 \right)^{1/4} F_{22} (\hat{\kappa}_1) }[/math]

so that

[math]\displaystyle{ F_{22} (\hat{\kappa}_1) = \frac{1}{2} \int_{\hat{\kappa}_1}^{\infty} \frac{E(\hat{\kappa})}{\hat{\kappa}} \left( 1 + \frac{\hat{\kappa}_1^2}{\hat{\kappa}^2} \right) \, \mathrm{d} \hat{\kappa} }[/math] .

These two one-dimensional spectra are related to each other by

[math]\displaystyle{ F_{22} (\hat{\kappa}_1)= \frac{1}{2} \left( F_{11} (\hat{\kappa}_1) - \hat{\kappa}_1 \frac{\mathrm{d}F_{11}(\hat{\kappa}_1)}{\mathrm{d}\hat{\kappa}_1} \right) }[/math]

and, thus, [math]\displaystyle{ F_{22}=\frac{4}{3} F_{11} }[/math] in the inertial subrange. These relationships hold for any direction of profiling, as long as we refer to the velocity component that is parallel to the direction of profiling by the subscripts ([math]\displaystyle{ _{11} }[/math]) and the (mutually orthogonal) pair of velocity components that are orthogonal to the direction of profiling using the subscripts ([math]\displaystyle{ _{22} }[/math]). Thus, the second orthogonal velocity component has the spectrum [math]\displaystyle{ E_{33}\equiv E_{22} }[/math] .

Spectra of velocity gradients

The spectra of the gradients of velocity are closely related to the rate of dissipation, [math]\displaystyle{ \varepsilon }[/math], and are often called dissipation spectra. These spectra are the velocity spectra multiplied by [math]\displaystyle{ \kappa^2 }[/math] or [math]\displaystyle{ \kappa_1^2 }[/math], whichever is appropriate. The rate of dissipation is related to the gradient of the three-dimensional velocity spectrum by

[math]\displaystyle{ \begin{equation} \begin{split} \varepsilon &= 2\nu \int_0^{\infty} \kappa^2 E(\kappa)\, \mathrm{d} \kappa = 2\nu \left(\varepsilon\nu^5 \right)^{1/4} \int_0^{\infty} \kappa^2 F(\hat{\kappa})\, \mathrm{d} \kappa \\ &=2\nu \left(\varepsilon\nu^5 \right)^{1/4} L_K^{-3} \int_0^{\infty} \hat{\kappa}^2 F(\hat{\kappa})\, \mathrm{d} \hat{\kappa} \\ &= 2\varepsilon \int_0^{\infty} G(\hat{\kappa})\, \mathrm{d} \hat{\kappa} \end{split} \end{equation} }[/math]

Thus, the universal (non-dimensional) gradient spectrum is [math]\displaystyle{ G=\hat{\kappa}^2 F }[/math] , and its integral over all wavenumbers must equal 1/2. The along-profile gradient of the along-profile velocity fluctuations often called the rate of strain (or, simply strain), is related to the rate of dissipation by

[math]\displaystyle{ \begin{equation} \begin{split} \varepsilon &= 15\nu \int_0^{\infty} \kappa_1^2 E_{11}(\kappa_1)\, \mathrm{d}\kappa_1 = 15\nu \left(\varepsilon\nu^5 \right)^{1/4} \int_0^{\infty} \kappa_1^2 F_{11} (\hat{\kappa}_1)\, \mathrm{d} \kappa_1 \\ &= 15\varepsilon \int_0^{\infty} G_{11} (\hat{\kappa}_1)\, \mathrm{d} \hat{\kappa}_1 \end{split} \end{equation} }[/math]

where [math]\displaystyle{ G_{11}=\hat{\kappa}_1^2 F_{11} }[/math] is the universal (and non-dimensional) rate of strain spectrum, which must integrate to 1/15. Similarly, the shear spectrum is related to the rate of dissipation by

[math]\displaystyle{ \begin{equation} \begin{split} \varepsilon &= \frac{15}{2} \nu \int_0^{\infty} \kappa_1^2 E_{22}(\kappa_1)\, \mathrm{d}\kappa_1 = \frac{15}{2}\nu \left(\varepsilon\nu^5 \right)^{1/4} \int_0^{\infty} \kappa_1^2 F_{22}\, (\hat{\kappa}_1) \mathrm{d} \kappa_1 \\ &= \frac{15}{2}\varepsilon \int_0^{\infty} G_{22} (\hat{\kappa}_1)\, \mathrm{d} \hat{\kappa}_1 \end{split} \end{equation} }[/math]

where [math]\displaystyle{ G_{22}= \hat{\kappa}_1^2 F_{22} }[/math] is the universal shear spectrum which must integrate to 2/15.

Spectra in the inertial subrange

In the inertial subrange, the three-dimensional velocity spectrum follows a power-law behaviour and this makes it possible to easily derive the one-dimensional spectra, in this range. Using ( ?) within the inertial subrange gives

[math]\displaystyle{ \tilde{F}_{11} (\hat{\kappa}_1) = \int_{\hat{\kappa}_1}^{\infty} \frac{F(\hat{\kappa})}{\hat{\kappa}} \left(1 - \frac{\hat{\kappa}_1^2}{\hat{\kappa}^2} \right)\, \mathrm{d}\hat{\kappa} = \frac{18}{55} C \hat{\kappa}_1^{-5/3} = C_1 \hat{\kappa}_1^{-5/3} }[/math]

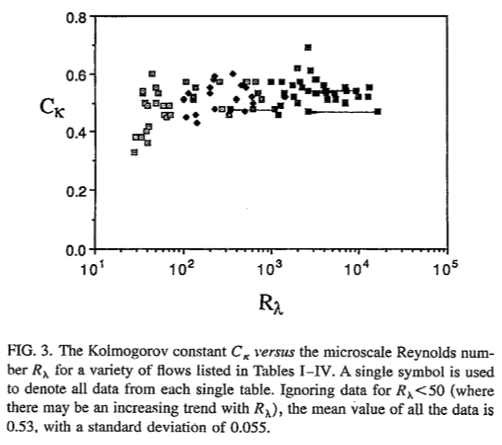
where [math]\displaystyle{ C_1=18C/55\approx27/55 }[/math] is frequently called the one-dimensional Kolmogorov constant, and the tilde is used to indicate these equations apply only in the inertial subrange. It is not possible to measure the three-dimensional spectrum and, thus, it is not possible to estimate [math]\displaystyle{ C }[/math] directly. Consequently, there is research interest in estimating </math>C_1</math> because it is the only practical way to determine the three-dimensional Kolmogorov constant [math]\displaystyle{ C }[/math]. Sreenivasa (1995) compiled the values of the one-dimensional Kolmogorov constant reported from a wide range of measurements in the atmosphere, ocean, wind tunnels and pipes. The mean value (excluding low Reynolds number measurements) is [math]\displaystyle{ 0.53 }[/math] and the standard deviation is [math]\displaystyle{ 0.055 }[/math] (Figure 1). A crude estimate of the [math]\displaystyle{ 95\% }[/math] confidence interval is [math]\displaystyle{ C_1=0.53\pm0.03 }[/math].

Figure 1. Figure 3 from Sreenivasa (1995) for the estimates of the one-dimensional Kolmogorov constant, [math]\displaystyle{ C_1 }[/math], derived from experimental measurements of along-stream velocity measurements and/or the rate of strain.

Using [math]\displaystyle{ \tilde{F}_{22}= \frac{4}{3} \tilde{F}_{11} }[/math], the one-dimensional spectrum for the velocity components that are orthogonal to the direction of profiling is

[math]\displaystyle{ \tilde{F}_{22} (\hat{\kappa}_1) = \frac{4}{3} C_1 \hat{\kappa}_1^{-5/3} }[/math]

The gradient spectra in the inertial subrange are

[math]\displaystyle{ \begin{equation} \tilde{G}_{11} (\hat{\kappa}_1) = C_1 \hat{\kappa}_1^{1/3} \end{equation} }[/math]

and

[math]\displaystyle{ \begin{equation} \tilde{G}_{22} (\hat{\kappa}_1) = \frac{4}{3} C_1 \hat{\kappa}_1^{1/3} \end{equation} }[/math]

Units of a wavenumber spectrum

There are two commonly used units for a wavenumber and it is important to be clear about which one you are using because the level of a spectrum depends on the unit. Mathematicians and theoreticians usually use ‘angular’ units expressed in radians and this should be indicated by [math]\displaystyle{ \mathrm{rad\, m^{-1}} }[/math] -– radians per meter. It is the counterpart to frequency expressed in [math]\displaystyle{ \mathrm{rad\, s^{-1}} }[/math] -– radians per second. Never express the units as [math]\displaystyle{ \mathrm{m^{-1}} }[/math] just because an angle technically has no units. This usage is ambiguous. The other unit, which is preferred by investigational scientists because it is derived naturally by a Fourier transform, among other reasons, is [math]\displaystyle{ \mathrm{cpm} }[/math] -– cycles per meter. It is the counterpart of [math]\displaystyle{ \mathrm{Hz} }[/math] -– cycles per second. The two measures of wavenumber differ by a factor of [math]\displaystyle{ 2\pi }[/math] which is not small compared to one. Here we use the symbol [math]\displaystyle{ \kappa }[/math] to indicate a wavenumber expressed in units of [math]\displaystyle{ \mathrm{rad\, m^{-1}} }[/math], and we use the symbol [math]\displaystyle{ k }[/math] to indicate a wavenumber in units of [math]\displaystyle{ \mathrm{cpm} }[/math]. Their relationship is

[math]\displaystyle{ \kappa = 2 \pi k }[/math]

Regardless of the unit of wavenumber that you employ, the integral over a wavenumber band gives the variance within that band and this variance must be wavenumber-unit independent. Here are some examples that apply in the inertial subrange. For the velocity spectrum, we must have

[math]\displaystyle{ F_{22}(\hat{k}_1) \mathrm{d}\hat{k}_1 = F_{22} (\hat{\kappa}_1)\, \mathrm{d} \hat{\kappa}_1 }[/math]

and substituting ( ) gives

[math]\displaystyle{ \begin{equation} \begin{split} \tilde{F}_{22} (\hat{k}_1) \, \mathrm{d}\hat{k}_1 &= \frac{4}{3} C_1 \left(2\pi \hat{k}_1 \right)^{-5/3} \mathrm{d} (2\pi\hat{k}_1 ) \\ &= \left(2\pi\right)^{-2/3}\, \frac{4}{3} C_1 \,\hat{k}_1^{-5/3}\, \mathrm{d}\hat{k}_1 \end{split} \end{equation} }[/math]

which means that, in the inertial subrange, the cross-profile spectrum of velocity, [math]\displaystyle{ \tilde{F}_{22}(\hat{k}_1) }[/math], expressed in units of [math]\displaystyle{ \mathrm{cpm} }[/math], is smaller than the same spectrum, [math]\displaystyle{ \tilde{F}_{22}(\hat{\kappa}_1) }[/math], expressed in units of [math]\displaystyle{ \mathrm{rad\, m^{-1}} }[/math].

Similarly, the universal shear spectrum, using ( ) is

[math]\displaystyle{ \begin{equation} \begin{split} \tilde{G}_{22} (\hat{k}_1) \, \mathrm{d}\hat{k}_1 &= \frac{4}{3} C_1 \left(2\pi \hat{k}_1 \right)^{1/3} \mathrm{d} (2\pi\hat{k}_1 ) \\ &= \left(2\pi\right)^{4/3}\, \frac{4}{3} C_1 \,\hat{k}_1^{1/3}\, \mathrm{d}\hat{k}_1 \end{split} \end{equation} }[/math]

which means that the shear spectrum, expressed in units of [math]\displaystyle{ \mathrm{cpm} }[/math], is larger by a factor of [math]\displaystyle{ (2\pi)^{4/3} }[/math] in the inertial subrange than the shear spectrum expressed in units of [math]\displaystyle{ \mathrm{rad\, m^{-1}} }[/math]. Finally, the complete shear spectrum must integrate to 2/15 over all wavenumbers and, therefore, the peak of the shear spectrum expressed in units of [math]\displaystyle{ \mathrm{cpm} }[/math] is larger than the shear spectrum expressed in units of [math]\displaystyle{ \mathrm{rad\, m^{-1}} }[/math] by a factor of [math]\displaystyle{ 2\pi }[/math].

Estimating [math]\displaystyle{ \varepsilon }[/math] by spectral integration

The shear probe provides a measure of the turbulent shear, and this data can be used to estimate the spectrum of the shear. The variance of shear is often estimated by integrating the spectrum of shear, namely

[math]\displaystyle{ \varepsilon = \frac{15}{2}\nu \overline{\left(\frac{\partial u}{\partial z} \right)^2} \equiv \frac{15}{2}\nu \int_0^{\infty} \Phi(k) \,\mathrm{d}k \approx \frac{15}{2}\nu \int_0^{k_u} \Phi(k) \,\mathrm{d}k }[/math]

where [math]\displaystyle{ \Phi }[/math] is an estimate of the spectrum of shear, [math]\displaystyle{ \Psi }[/math], and the upper limit of spectral integration, [math]\displaystyle{ k_u }[/math], is imposed by practical considerations. Thus, only a fraction of the shear variance is resolved by this method. There is value in having a mathematical approximation for the spectrum of shear and for the fraction of the variance that is resolved by integration to a finite upper wavenumber. The model spectrum provides a gauge for judging the quality of the estimate of the spectrum. The model of its integral provides a means to correct (upwards) the estimate of [math]\displaystyle{ \varepsilon }[/math] provided by spectral integration up to a finite wavenumber. Details of spectral integration are discussed here.

New approximation of the shear spectrum

Lueck (2021a) used data collected in a tidal channel to produce approximately 14000 spectra. Each spectrum spanned [math]\displaystyle{ 5\,\mathrm{m} }[/math] of flow, and each one was individually non-dimensionalized using the estimated rate of dissipation for that [math]\displaystyle{ 5\,\mathrm{m} }[/math] segment (Figures 5 and 6). The mathematical approximation of the average shear spectrum is

Figure 5. The [math]\displaystyle{ 14676 }[/math] spectra reported by Lueck (2021b) (grey dots), their bin averages (black disks), the second Nasmyth model (dotted line) and the model [math]\displaystyle{ \Psi_L }[/math] (solid line).

Figure 6. Same as previous figure but in linear space.

[math]\displaystyle{ \begin{equation} \begin{split} \Psi_L(\hat{k}_1) &= \left( \frac{8.048\,\hat{k}_{1}^{1/3}}{1+ \left(21.7\,\hat{k}_1 \right)^3} \right) \left( \frac{1}{1+ \left(6.6\,\hat{k}_{1} \right)^{5/2}} \right) \left(1+ \frac{0.36\,y}{\left(y-1 \right)^2 + 2y} \right) \\ y &= \left(\frac{\hat{k}_1}{0.0152}\right)^2 \end{split} \end{equation} }[/math]

which integrates to a value that is [math]\displaystyle{ 1\% }[/math] larger than [math]\displaystyle{ 15/2 }[/math]. The one-dimensional Kolmogorov constant is [math]\displaystyle{ C_1=0.52 }[/math] for this model. An approximation for the integral of this spectrum is

[math]\displaystyle{ I_L(\hat{k}_1) = \frac{15}{2} \int_0^{\hat{k}_1} \Psi_L(\xi) \,\mathrm{d}\xi = \tanh \left(65.5\,\hat{k}_1^{4/3}\right) - 19\,\hat{k}_1^{4/3} \exp\left(-54.5\,\hat{k}_1^{4/3} \right) }[/math]

A major purpose of a mathematical model of a shear spectrum is to compare it to an estimated spectrum to test the quality of the estimate. Such a test also requires knowledge of the statistical uncertainty of a spectral estimate. The deviation of a spectrum from a model spectrum, normalized by the expected standard deviation of the estimate provides a quality control metric.

The [math]\displaystyle{ \approx14000 }[/math] spectra of were averaged into 21 bins spaced uniformly in the logarithm of their wavenumber. The maximum deviations of the three spectral models from the bin averages of the spectra are [math]\displaystyle{ 0.3 }[/math], [math]\displaystyle{ 0.2 }[/math] and [math]\displaystyle{ 0.1 }[/math], for the approximations [math]\displaystyle{ \Psi_{N_1} }[/math], [math]\displaystyle{ \Psi_{N_2} }[/math], and [math]\displaystyle{ \Psi_L }[/math], respectively (Figure 7). The mean absolute deviations are [math]\displaystyle{ 0.11 }[/math], [math]\displaystyle{ 0.07 }[/math] and [math]\displaystyle{ 0.014 }[/math], respectively. The peak of the shear spectrum is [math]\displaystyle{ 2.3 }[/math], and therefore the approximation [math]\displaystyle{ \Psi_{N_1} }[/math] deviate by less than [math]\displaystyle{ 5\% }[/math] from the bin averages relative to this reference. However, [math]\displaystyle{ \Psi_L }[/math] provides a closer approximation to the bin averages.

The major purpose of a mathematical model of the integral of the shear spectrum is to use it to determine the fraction of the variance that has been resolved by integrating the spectrum to only a finite wavenumber, [math]\displaystyle{ k_u }[/math].

Figure 7. The deviation of the spectral approximations [math]\displaystyle{ \Psi_{N_1} }[/math] (squares), [math]\displaystyle{ \Psi_{N_2} }[/math] (disks), and [math]\displaystyle{ \Psi_L }[/math] (triangles) from the bin averages, [math]\displaystyle{ \mu }[/math], of the approximately [math]\displaystyle{ 14700 }[/math] non-dimensions spectra reported by Lueck 2021b. The grey shading is the [math]\displaystyle{ 95\% }[/math] bootstrap confidence interval around the bin averages. The mean average deviations (MAD) are indicated for each approximation.