Spectra in the inertial subrange: Difference between revisions
KikiSchulz (talk | contribs) Created page with "{{DefineConcept |description=In the inertial subrange, the three-dimensional velocity spectrum follows a power-law behaviour and this makes it possible to easily derive the on..." |
KikiSchulz (talk | contribs) No edit summary |
||
| Line 35: | Line 35: | ||
\end{equation} | \end{equation} | ||
</math> | </math> | ||
You want more? Go to [[Spectral integration]] | |||
Latest revision as of 22:27, 9 November 2021
| Short definition of Spectra in the inertial subrange |
|---|
| In the inertial subrange, the three-dimensional velocity spectrum follows a power-law behaviour and this makes it possible to easily derive the one-dimensional spectra, in this range |
This is the common definition for Spectra in the inertial subrange, but other definitions maybe discussed within the wiki.
In the inertial subrange, the three-dimensional velocity spectrum follows a power-law behaviour and this makes it possible to easily derive the one-dimensional spectra, in this range. Using ( ?) within the inertial subrange gives
where
Using
The gradient spectra in the inertial subrange are
and
You want more? Go to Spectral integration
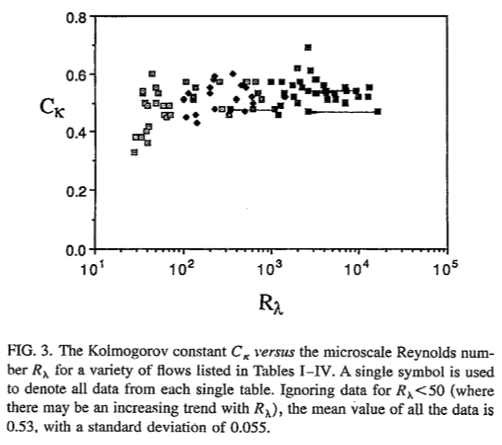
- ↑ Jump up to: 1.0 1.1 Sreenivasan, K. R. (1995). On the universality of the Kolmogorov constant. Physics of Fluids, 7(11), 2778-2784.
