Along-beam bin center separation: Difference between revisions
Jmmcmillan (talk | contribs) Created page with "[PLACEHOLDER -- NEED TO CONFIRM THIS IS CORRECT AND/OR ADD PICTURE] For ADCPs, the <math>Z</math>-axis in instrument coordinates is commonly defined along the axis of the ADC..." |
Yuengdjern (talk | contribs) No edit summary |
||
| (8 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
For ADCPs, the <math>Z</math>-axis in instrument coordinates is commonly defined along the axis of the ADCP pressure case. The velocity data are commonly given in terms of this <math>Z</math>-coordinate. For a vertical beam, the along beam bin center separation (<math>r_0</math>) is given by: | For ADCPs, the <math>Z</math>-axis in instrument coordinates is commonly defined along the axis of the ADCP pressure case. The velocity data are commonly given in terms of this <math>Z</math>-coordinate. For a vertical beam, the along beam bin center separation (<math>r_0</math>) is given by: | ||
<math>r_0 = \ | <math>\delta r_0 = \delta z</math> | ||
where <math>\ | where <math>\delta z</math> is the distance between bin-centers along the <math>Z</math>-axis. | ||
For diverging beams, the along beam bin center separation (<math>r_0</math>) is given by: | For diverging beams, the along beam bin center separation (<math>r_0</math>) is given by: | ||
<math>r_0 = \frac{\ | <math>\delta r_0 = \frac{\delta z}{\cos\theta}</math> | ||
where <math>\theta</math> is the angle of the diverging beams with the <math>Z</math>-axis. | where <math>\theta</math> is the angle of the diverging beams with the <math>Z</math>-axis. | ||
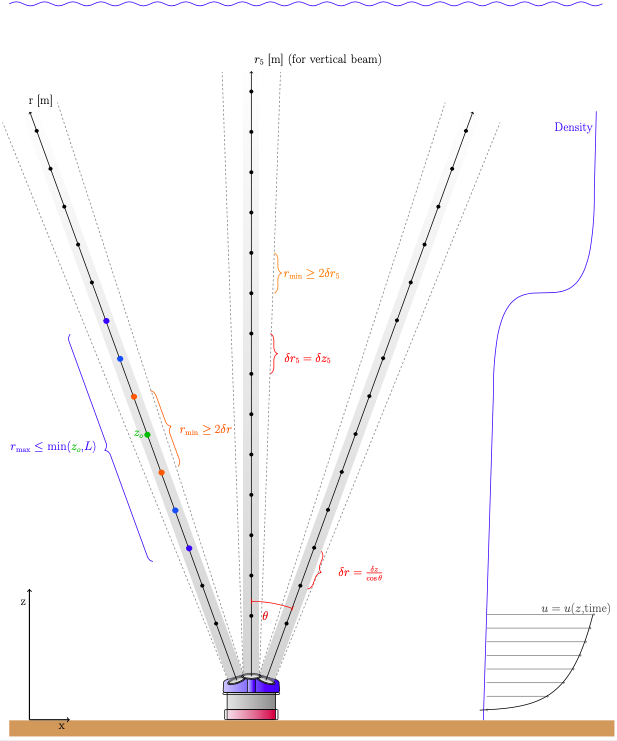
[[File:SF atomix ADCP.png|frame| Schematic of ADCP and its beams, showing the difference between the vertical co-ordinate <math> z </math> and the along-beam radial distances <math> r </math>]] | |||
[[Category:Velocity profilers]] | |||
Go back to [[Processing your ADCP data using structure function techniques | Compute structure functions and dissipation estimates]] | |||
Latest revision as of 10:41, 10 December 2021
For ADCPs, the [math]\displaystyle{ Z }[/math]-axis in instrument coordinates is commonly defined along the axis of the ADCP pressure case. The velocity data are commonly given in terms of this [math]\displaystyle{ Z }[/math]-coordinate. For a vertical beam, the along beam bin center separation ([math]\displaystyle{ r_0 }[/math]) is given by:
[math]\displaystyle{ \delta r_0 = \delta z }[/math]
where [math]\displaystyle{ \delta z }[/math] is the distance between bin-centers along the [math]\displaystyle{ Z }[/math]-axis.
For diverging beams, the along beam bin center separation ([math]\displaystyle{ r_0 }[/math]) is given by:
[math]\displaystyle{ \delta r_0 = \frac{\delta z}{\cos\theta} }[/math]
where [math]\displaystyle{ \theta }[/math] is the angle of the diverging beams with the [math]\displaystyle{ Z }[/math]-axis.
Go back to Compute structure functions and dissipation estimates
