Decomposing velocity measurements: Difference between revisions

From Atomix
← Older edit
Visual
 
(25 intermediate revisions by the same user not shown)
Line 4: Line 4:
}}
}}


The quality-controlled velocities are first [[Detrending time series|detrended]] before being further analysed to determine [[Velocity past the sensor|mean flow past the sensor]] and [[Surface wave statistics|surface wave statistics]]. These quantities are necessary for later choosing the appropriate [[Velocity inertial subrange model| inertial subrange model]] for [[Spectral fitting|spectral fitting]].
The quality-controlled velocities can be [[Detrending time series|detrended]] before being further analysed to determine [[Velocity past the sensor|mean flow past the sensor]] and [[Surface wave statistics|surface wave statistics]]. These quantities are necessary for later choosing the appropriate [[Velocity inertial subrange model| inertial subrange model]] for [[Spectral fitting|spectral fitting]].
Quality-controlled velocities may also need to be detrended before applying various [[Velocity despiking|despiking]]. Because estimating <math>\varepsilon</math> is done from the spectral observations, the analysis is insensitive to this step provided that we don’t filter out the scales shorter than the [[Segmenting datasets| segment length]].
==Methods for detrending==
 
<div><ul>
<li style="display: inline-block; vertical-align: top;"> [[File:Short timeseries.png|thumb|none|350px|512 s segment of the measured velocities after applying different [[Detrending time series|detrending methods]]]]
</li>
<li style="display: inline-block; vertical-align: top;"> [[File:Short_spectra.png|thumb|none|350px|Example velocity spectra of the short 512 s of records before and after different detrending techniques applied to the original 6h  time series. The impact of the detrending method can be seen at the lowest frequencies only]] </li>
</ul></div>


There is no exact definition for what consists of a "trend", nor any set algorithm for identifying the trend. The following techniques can be used for detrending <ref name=Wuetal_PNAS/>:
# Linear trend removal
# Low-pass linear filters (e.g., butterworth filter)
# Empirical modal decomposition


The first two methods presume the original time series is [[Stationarity|stationary]] and linear, while the third is adaptive and applicable to nonlinear and non-stationary timeseries.


[[File:Long timeseries.png|thumb|none|600px|Measured velocities at 4 Hz from an [[Acoustic-Doppler Velocimeters]] have been detrended using three different techniques. Empirical modal decomposition (EMD) <ref name="Wuetal_PNAS">{{Cite journal
|authors=Zhaohua Wu, Norden E. Huang, Steven R. Long, and Chung-Kang Peng
|journal_or_publisher=PNAS
|paper_or_booktitle=On the trend, detrending, and variability of nonlinear and nonstationary time series
|year=2007
|doi=10.1073/pnas.0701020104
}}</ref>, linear trend, and a 2nd order low-pass Butterworth filter. A cut-off period of 10 min was targeted by both the filter and EMD]]


===Long continuous sampling===
'''Info needs simplifying after convening as a subgroup'''
Different techniques dependent on whether measurements were collected continuously or in long bursts (define here).


===Short burst sampling===
A short burst is typically at most 2-3x the expected largest turbulence length scales. As a rule of thumb, turbulence estimates from the inertial subrange of velocity rely on 5 to 15 min long-segments. ``` Act of segmenting is effectively a form of filtering'''
* Linear trend removal
* Empirical mode decomposition (nonlinear and/or non-stationary signal)


==Notes==
----
----
Return to [[Velocity_point-measurements|Velocity point-measurements' welcome page]]
Return to [[Preparing quality-controlled velocities]]

Latest revision as of 19:08, 5 July 2022


The quality-controlled velocities can be detrended before being further analysed to determine mean flow past the sensor and surface wave statistics. These quantities are necessary for later choosing the appropriate inertial subrange model for spectral fitting. Quality-controlled velocities may also need to be detrended before applying various despiking. Because estimating [math]\displaystyle{ \varepsilon }[/math] is done from the spectral observations, the analysis is insensitive to this step provided that we don’t filter out the scales shorter than the segment length.

  • 512 s segment of the measured velocities after applying different detrending methods
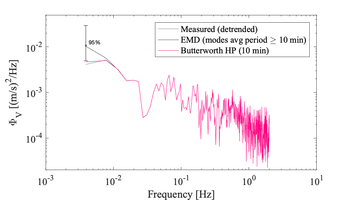
  • Example velocity spectra of the short 512 s of records before and after different detrending techniques applied to the original 6h time series. The impact of the detrending method can be seen at the lowest frequencies only




Return to Preparing quality-controlled velocities

Retrieved from "http://atomix.app.uib.no/index.php?title=Decomposing_velocity_measurements&oldid=4287"