Velocity despiking: Difference between revisions

From Atomix
← Older editNewer edit →
VisualWikitext
mNo edit summary
m Fixed headings
Line 14: Line 14:
</ul></div>
</ul></div>


= Despiking methods =
Several techniques exist for despiking. The most used with  [[Acoustic-Doppler Velocimeters| acoustic-Doppler velocimeters]] are the phase-space thresholding techniques <ref name="GoringNikora"/>. Other techniques currently being investigated by the subgroup are those used in atmospheric turbulence studies <ref name="Starkenburg">{{Cite journal|authors= D. Starkenburg, S. Metzger, G.J. Fochesatto, J.G Alfieri, R. Gens, A. Prakash and J. Cristobal|journal_or_publisher=  J. Atmos. Oceanic Technoly|paper_or_booktitle= Assessment of Despiking Methods for Turbulence Data in Micrometeorology
Several techniques exist for despiking. The most used with  [[Acoustic-Doppler Velocimeters| acoustic-Doppler velocimeters]] are the phase-space thresholding techniques <ref name="GoringNikora"/>. Other techniques currently being investigated by the subgroup are those used in atmospheric turbulence studies <ref name="Starkenburg">{{Cite journal|authors= D. Starkenburg, S. Metzger, G.J. Fochesatto, J.G Alfieri, R. Gens, A. Prakash and J. Cristobal|journal_or_publisher=  J. Atmos. Oceanic Technoly|paper_or_booktitle= Assessment of Despiking Methods for Turbulence Data in Micrometeorology
|year= 2016|doi= 10.1175/JTECH-D-15-0154.1􏰐}}</ref>, in particular the median filter despiking technique <ref name="Brock">{{Cite journal|authors=F.V. Brock|journal_or_publisher=  J. Atmos. Oceanic Technoly|paper_or_booktitle= A nonlinear filter to remove impulse noise from meteorological data
|year= 2016|doi= 10.1175/JTECH-D-15-0154.1􏰐}}</ref>, in particular the median filter despiking technique <ref name="Brock">{{Cite journal|authors=F.V. Brock|journal_or_publisher=  J. Atmos. Oceanic Technoly|paper_or_booktitle= A nonlinear filter to remove impulse noise from meteorological data
|year= 1986|doi= 10.1175/1520-0426(1986)003,0051:ANFTRI.2.0.CO;2􏰐}}</ref>. This method derives its threshold for identifying spurious spikes from the dataset.
|year= 1986|doi= 10.1175/1520-0426(1986)003,0051:ANFTRI.2.0.CO;2􏰐}}</ref>. This method derives its threshold for identifying spurious spikes from the dataset.


==Filter based methods==
=Filter based methods=
This category of methods is quite common in the literature and have been reviewed extensively by others  <ref name="GoringNikora"/><ref name="Starkenburg"/>. These methods compare the original signal against a smoothed version, and values exceeding a threshold <math>T</math> are deemed to be spikes. Most commonly, the threshold is applied to the timeseries of [[:Media:Smoothed velocities.png|velocity differences]] obtained by subtracting the smoothed velocities from the original spiky signal.  
This category of methods is quite common in the literature and have been reviewed extensively by others  <ref name="GoringNikora"/><ref name="Starkenburg"/>. These methods compare the original signal against a smoothed version, and values exceeding a threshold <math>T</math> are deemed to be spikes. Most commonly, the threshold is applied to the timeseries of [[:Media:Smoothed velocities.png|velocity differences]] obtained by subtracting the smoothed velocities from the original spiky signal.  


Line 34: Line 33:
[[File:Threshold logic Brock1986.png|thumb|Histogram of velocity differences. The local minimum denotes the lower and upper thresholds <math>T</math> for identifying spikes. The standard deviation of the original timeserie is 2 cm/s.]]
[[File:Threshold logic Brock1986.png|thumb|Histogram of velocity differences. The local minimum denotes the lower and upper thresholds <math>T</math> for identifying spikes. The standard deviation of the original timeserie is 2 cm/s.]]


==Phase-space thresholding methods==
=Phase-space thresholding methods=
'''Elaborate a bit? Or include information in a separate page'''
'''Elaborate a bit? Or include information in a separate page'''


Revision as of 23:59, 24 November 2021


Overview

Any measured signal may be contaminated by spikes. These spikes are typically short-lived and transient, which result in sudden change in the measured velocities.

Spikes in velocities measured by acoustic-Doppler velocimeters can result from aliasing of the Doppler signal, in particular when pulses become contaminated by reflecting from complex objects and boundaries [1]. These spikes must be removed because they can alter quite dramatically the velocity spectra, which is then used for fitting inertial subrange model.

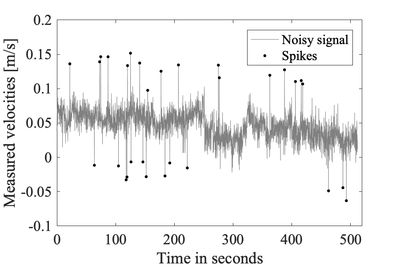
  • Example velocities measured by an acoustic-Doppler velocimeters
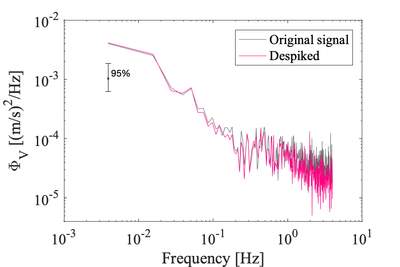
  • Example velocity spectra before and after removing spikes. The variance of the despiked signal has reduced by 12% even though there were 30 spikes

Several techniques exist for despiking. The most used with acoustic-Doppler velocimeters are the phase-space thresholding techniques [1]. Other techniques currently being investigated by the subgroup are those used in atmospheric turbulence studies [2], in particular the median filter despiking technique [3]. This method derives its threshold for identifying spurious spikes from the dataset.

Filter based methods

This category of methods is quite common in the literature and have been reviewed extensively by others [1][2]. These methods compare the original signal against a smoothed version, and values exceeding a threshold [math]\displaystyle{ T }[/math] are deemed to be spikes. Most commonly, the threshold is applied to the timeseries of velocity differences obtained by subtracting the smoothed velocities from the original spiky signal.

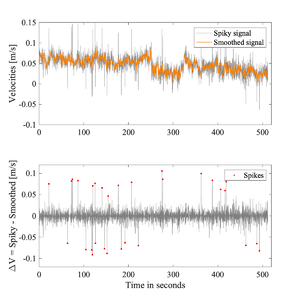
Example velocities before and after smoothing (top). Filter-based despiking methods use the difference between these two signals to identify spikes (bottom).

Filter choice

In the 1970s, scientists developed methods based on nonlinear median filters [4]. These filters are less biased by spikes than other linear operations such as low-pass butterworth filters[2]. The moving median filter, for example, only requires a window size, i.e, the number of points over which to calculate the median. This size must be longer than the duration of spikes, which can span consecutive samples. This number must also be sufficiently short to compute a reasonable local median (see Table 1 of Starkenburg et al 2016[2]). The challenge then becomes determining the threshold for identifying spikes.

Identifying the threshold

Some filter-based methods use thresholds based on a factor of the original timeseries' standard deviation (e.g., Tukey method discussed by Goring & Nikora[1]). The results of the analysis then becomes sensitive to this choice of factor. A more automated means to identify the threshold was proposed by Brock (1986)[3] using a histogram of velocity differences.

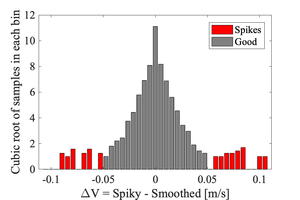
Histogram of velocity differences. The local minimum denotes the lower and upper thresholds [math]\displaystyle{ T }[/math] for identifying spikes. The standard deviation of the original timeserie is 2 cm/s.

Phase-space thresholding methods

Elaborate a bit? Or include information in a separate page

Notes

  1. ↑ 1.0 1.1 1.2 1.3 D. G. Goring and V.I. Nikora. 2002. Despiking Acoustic Doppler Velocimeter Data. Journal of Hydraulic Engineering. doi:10.1061/􏰠ASCE􏰐0733-9429􏰠2002􏰐128:1􏰠117􏰐
  2. ↑ 2.0 2.1 2.2 2.3 D. Starkenburg, S. Metzger, G.J. Fochesatto, J.G Alfieri, R. Gens and A. Prakash and J. Cristobal. 2016. Assessment of Despiking Methods for Turbulence Data in Micrometeorology. J. Atmos. Oceanic Technoly. doi:10.1175/JTECH-D-15-0154.1􏰐
  3. ↑ 3.0 3.1 F.V. Brock. 1986. A nonlinear filter to remove impulse noise from meteorological data. J. Atmos. Oceanic Technoly. doi:10.1175/1520-0426(1986)003,0051:ANFTRI.2.0.CO;2􏰐
  4. ↑ A.E. Beaton and J.W. Tukey. 1974. The fitting of power series, meaning polynomials, illustrated on band-spectroscopic data. Technometrics. doi:10.1080/00401706.1974.10489171

Return to Velocity point-measurements' welcome page

Retrieved from "http://atomix.app.uib.no/index.php?title=Velocity_despiking&oldid=2690"