Processing your ADCP data using structure function techniques

To calculate the dissipation rate at a specific range bin and a specific time ensemble:

Schematic showing along-beam distance $r$ and radial velocities.

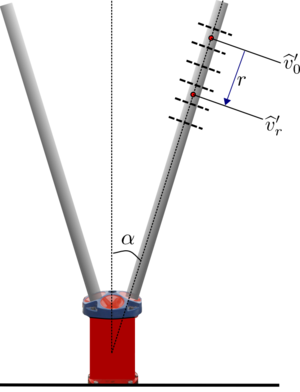
1. Extract or compute the along-beam bin center separation [$\delta r_0$] based on the instrument geometry
2. Calculate the along-beam velocity fluctuation time-series in each bin $n$, where [Failed to parse (syntax error): {\displaystyle b’(n, t_s)} ] from the along-beam velocity data that has met the QC criteria (i.e. the data in Level 2 of the netcdf file). Note $t_s$ is the timeseries index within a segment.
3. Select the maximum distance ($r_{max}$) over which to compute the structure function based on conditions of the flow (e.g., expected max overturn, spectral range corresponding to Failed to parse (unknown function "\math"): {\displaystyle k^{-5/3} <\math>). The corresponding number of bins is [<math>n_{\text{rmax}} = r_{max} / \delta r_0} ]
4. Calculate the structure function $D_{ll}$ for all possible bin separations $\delta$ within $r_{max}$ using either a bin-centred difference scheme or a forward-difference scheme.
5. Perform a regression of $D_{ll}(n,\delta )$ against $(\delta r{)}^{2/3}$ for the appropriate range of bins and $\delta$r separation distances. Be aware of special considerations for forward-difference, center-difference schemes in setting up the regression calculation. The regression is typically done as a least-squares fit, either as:
   
   $D_{ll}=a_0+a_1(\delta r{)}^{2/3}$;

or as

$D_{ll}=a_0+a_1(\delta r{)}^{2/3}+a_3((\delta r{)}^{2/3}{)}^3$

the former being the canonical method that excludes non-turbulent velocity differences between bins, whereas the latter is a modified method that includes non-turbulent velocity differences between bins due to any oscillatory signal (e.g. surface waves, motion of the ADCP on a mooring).

6. Use the coefficient $a_1$ to calculate $\epsilon$ as
   
   $\epsilon ={\left(\frac{a_1}{C_2}\right)}^{2/3}$
   
   where $C_2$ is an empirical constant, typically taken as 2.0 or 2.1.

---

Next step: Apply quality-control on dissipation rates (QA2)

Previous step: Apply quality-control on velocity time series data (QA1)

Return to ADCP Flow Chart front page