Processing your ADCP data using structure function techniques: Difference between revisions
From Atomix
mNo edit summary |
mNo edit summary |
||
| Line 1: | Line 1: | ||
To calculate the dissipation rate at a specific range bin and a specific time ensemble: | To calculate the dissipation rate at a specific range bin and a specific time ensemble: | ||
[[File:SF | [[File:ADCPschematic SF.png|thumb|Schematic showing along-beam distance <math> r </math> and radial velocities. ]] | ||
# Extract or compute the [[along-beam bin center separation]] [<math>r_0</math>] based on the instrument geometry | # Extract or compute the [[along-beam bin center separation]] [<math>r_0</math>] based on the instrument geometry | ||
| Line 10: | Line 10: | ||
# Use the coefficient <math>a_1</math> to calculate <math>\varepsilon</math> as <br /><br /> <math>\varepsilon = \left(\frac{a_1}{C_2}\right)^{2/3}</math> <br /><br /> where <math>C_2</math> is an [[ Structure function empirical constant | empirical constant]], typically taken as 2.0 or 2.1. | # Use the coefficient <math>a_1</math> to calculate <math>\varepsilon</math> as <br /><br /> <math>\varepsilon = \left(\frac{a_1}{C_2}\right)^{2/3}</math> <br /><br /> where <math>C_2</math> is an [[ Structure function empirical constant | empirical constant]], typically taken as 2.0 or 2.1. | ||
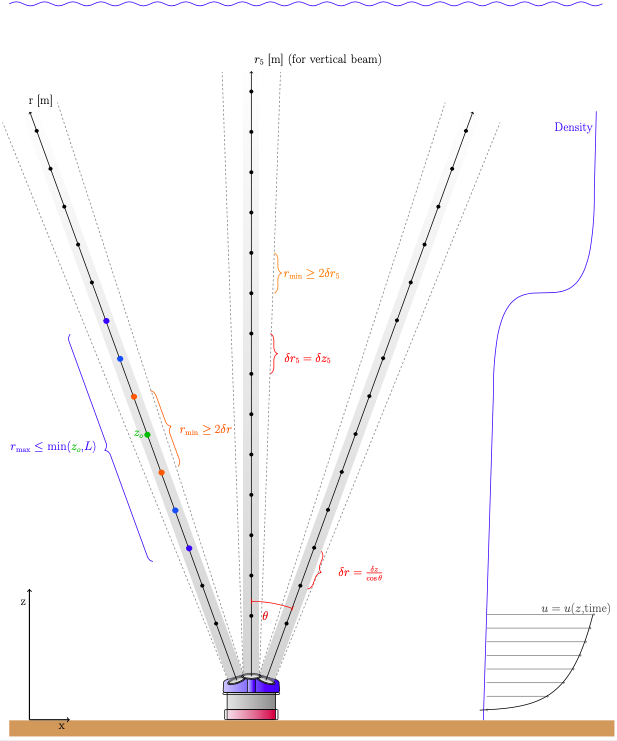
[[File:SF atomix ADCP.png|framed|Schematic showing the ADCP beam angles and the [[Nomenclature|variables]] used to define the structure function Dll.]] | |||
Schematic showing | |||
[[ | |||
---- | |||
Next step: [[Final data review (QA2) | Apply quality-control on dissipation rates (QA2)]] <br></br> | Next step: [[Final data review (QA2) | Apply quality-control on dissipation rates (QA2)]] <br></br> | ||
Previous step:[[Raw data review (QA1) | Apply quality-control on velocity time series data (QA1)]]<br></br> | Previous step:[[Raw data review (QA1) | Apply quality-control on velocity time series data (QA1)]]<br></br> | ||
Revision as of 18:56, 22 November 2021
To calculate the dissipation rate at a specific range bin and a specific time ensemble:
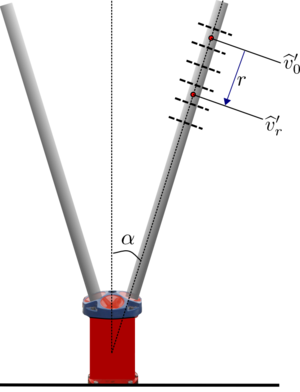
- Extract or compute the along-beam bin center separation [[math]\displaystyle{ r_0 }[/math]] based on the instrument geometry
- Calculate the along-beam velocity fluctuation time-series in each bin [math]\displaystyle{ n }[/math], where [[math]\displaystyle{ v’(n, t) }[/math]] from the along-beam velocity data that has met the QC criteria (i.e. the data in Level 2 of the netcdf file)
- Select the maximum distance ([math]\displaystyle{ r_{max} }[/math]) over which to compute the structure function based on conditions of the flow (e.g., expected max overturn). The corresponding number of bins is [[math]\displaystyle{ n_{\text{rmax}} = r_{max} / r_0 }[/math]]
- Calculate the structure function [math]\displaystyle{ D_{ll} }[/math] for all possible bin separations [math]\displaystyle{ \delta }[/math] using either a bin-centred difference scheme or a forward-difference scheme. Consider QA2 requirements when choosing differencing scheme.
- Perform a regression of [math]\displaystyle{ D_{ll}(n,\delta) }[/math] against [math]\displaystyle{ (\delta r_0)^{2/3} }[/math] for the appropriate range of bins and [math]\displaystyle{ \delta }[/math]r0 separation distances. Be aware of special considerations for forward-difference, center-difference schemes.
- Use the coefficient [math]\displaystyle{ a_1 }[/math] to calculate [math]\displaystyle{ \varepsilon }[/math] as
[math]\displaystyle{ \varepsilon = \left(\frac{a_1}{C_2}\right)^{2/3} }[/math]
where [math]\displaystyle{ C_2 }[/math] is an empirical constant, typically taken as 2.0 or 2.1.
Next step: Apply quality-control on dissipation rates (QA2)
Previous step: Apply quality-control on velocity time series data (QA1)
Return to ADCP Flow Chart front page
