Processing your ADCP data using structure function techniques: Difference between revisions
From Atomix
Yuengdjern (talk | contribs) No edit summary |
Yuengdjern (talk | contribs) No edit summary |
||
| Line 4: | Line 4: | ||
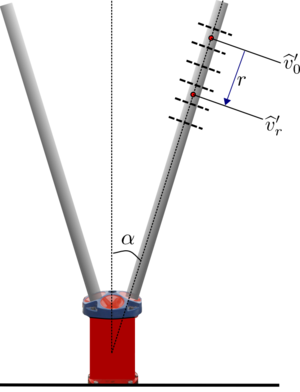
# Extract or compute the [[along-beam bin center separation]] [<math>\delta r_0</math>] based on the instrument geometry | # Extract or compute the [[along-beam bin center separation]] [<math>\delta r_0</math>] based on the instrument geometry | ||
# Calculate the [[along-beam velocity fluctuation]] time-series in each bin <math>n</math>, where [<math>b’(n, | # Calculate the [[along-beam velocity fluctuation]] time-series in each bin <math>n</math>, where [<math>b’(n, t_s)</math>] from the along-beam velocity data that has met the QC criteria (i.e. the data in Level 2 of the netcdf file). Note <math> t_s </math> is the timeseries index within a segment. | ||
# Select the maximum distance (<math>r_{max}</math>) over which to compute the structure function based on conditions of the flow (e.g., expected max overturn). The corresponding number of bins is [<math>n_{\text{rmax}} = r_{max} / \delta r_0</math>] | # Select the maximum distance (<math>r_{max}</math>) over which to compute the structure function based on conditions of the flow (e.g., expected max overturn). The corresponding number of bins is [<math>n_{\text{rmax}} = r_{max} / \delta r_0</math>] | ||
# Calculate the structure function <math>D_{ll}</math> for all possible bin separations <math>\delta</math> within <math>r_{max}</math> using either a [[bin-centred difference scheme]] or a [[forward-difference]] scheme. | # Calculate the structure function <math>D_{ll}</math> for all possible bin separations <math>\delta</math> within <math>r_{max}</math> using either a [[bin-centred difference scheme]] or a [[forward-difference]] scheme. | ||
Revision as of 15:10, 27 May 2022
To calculate the dissipation rate at a specific range bin and a specific time ensemble:
- Extract or compute the along-beam bin center separation [<math>\delta r_0</math>] based on the instrument geometry
- Calculate the along-beam velocity fluctuation time-series in each bin <math>n</math>, where [<math>b’(n, t_s)</math>] from the along-beam velocity data that has met the QC criteria (i.e. the data in Level 2 of the netcdf file). Note <math> t_s </math> is the timeseries index within a segment.
- Select the maximum distance (<math>r_{max}</math>) over which to compute the structure function based on conditions of the flow (e.g., expected max overturn). The corresponding number of bins is [<math>n_{\text{rmax}} = r_{max} / \delta r_0</math>]
- Calculate the structure function <math>D_{ll}</math> for all possible bin separations <math>\delta</math> within <math>r_{max}</math> using either a bin-centred difference scheme or a forward-difference scheme.
- Perform a regression of <math>D_{ll}(n,\delta)</math> against <math>(\delta r_0)^{2/3}</math> for the appropriate range of bins and <math>\delta</math>r0 separation distances. Be aware of special considerations for forward-difference, center-difference schemes in setting up the regression calculation. The regression is typically done as a least-squares fit, either as:
<math>D_{ll} = a_0 + a_1 (\delta r_0)^{2/3}</math>; or as
<math>D_{ll} = a_0 + a_1 (\delta r_0)^{2/3}+a_3((\delta r_0)^{2/3})^3 </math>
the former being the canonical method that excludes non-turbulent velocity differences between bins, whereas the latter is a modified method that includes non-turbulent velocity differences between bins due to any oscillatory signal (e.g. surface waves, motion of the ADCP on a mooring). - Use the coefficient <math>a_1</math> to calculate <math>\varepsilon</math> as
<math>\varepsilon = \left(\frac{a_1}{C_2}\right)^{2/3}</math>
where <math>C_2</math> is an empirical constant, typically taken as 2.0 or 2.1.
Next step: Apply quality-control on dissipation rates (QA2)
Previous step: Apply quality-control on velocity time series data (QA1)
Return to ADCP Flow Chart front page
