Spectra in the inertial subrange

Short definition of Spectra in the inertial subrange
In the inertial subrange, the three-dimensional velocity spectrum follows a power-law behaviour and this makes it possible to easily derive the one-dimensional spectra, in this range

This is the common definition for Spectra in the inertial subrange, but other definitions maybe discussed within the wiki.

{{#default_form:DefineConcept}} {{#arraymap:|,|x||}}

In the inertial subrange, the three-dimensional velocity spectrum follows a power-law behaviour and this makes it possible to easily derive the one-dimensional spectra, in this range. Using ( ?) within the inertial subrange gives

${\tilde{F}}_{11}({\hat{\kappa }}_1)=\underset{{\hat{\kappa }}_1}{\overset{\mathrm{\infty }}{\int }}\frac{F(\hat{\kappa })}{\hat{\kappa }}(1-\frac{{\hat{\kappa }}_1^2}{{\hat{\kappa }}^2})\mathrm{d}\hat{\kappa }=\frac{18}{55}C{\hat{\kappa }}_1^{-5/3}=C_1{\hat{\kappa }}_1^{-5/3}$

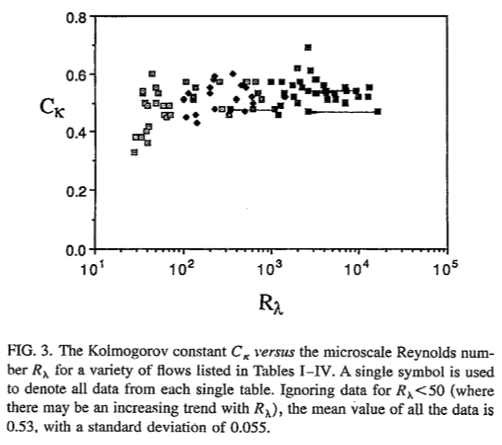
where $C_1=18C/55\approx 27/55$ is frequently called the one-dimensional Kolmogorov constant, and the tilde is used to indicate these equations apply only in the inertial subrange. It is not possible to measure the three-dimensional spectrum and, thus, it is not possible to estimate $C$ directly. Consequently, there is research interest in estimating </math>C_1</math> because it is the only practical way to determine the three-dimensional Kolmogorov constant $C$. Sreenivasa (1995) compiled the values of the one-dimensional Kolmogorov constant reported from a wide range of measurements in the atmosphere, ocean, wind tunnels and pipes. The mean value (excluding low Reynolds number measurements) is $0.53$ and the standard deviation is $0.055$ (Figure 1). A crude estimate of the $95\mathrm{\%}$ confidence interval is $C_1=0.53\pm 0.03$.

Figure 1. Figure 3 from Sreenivasa (1995) for the estimates of the one-dimensional Kolmogorov constant, $C_1$, derived from experimental measurements of along-stream velocity measurements and/or the rate of strain.

Using ${\tilde{F}}_{22}=\frac{4}{3}{\tilde{F}}_{11}$, the one-dimensional spectrum for the velocity components that are orthogonal to the direction of profiling is

${\tilde{F}}_{22}({\hat{\kappa }}_1)=\frac{4}{3}{C}_1{\hat{\kappa }}_1^{-5/3}$

The gradient spectra in the inertial subrange are

Failed to parse (unknown function "\begin{equation}"): {\displaystyle \begin{equation} \tilde{G}_{11} (\hat{\kappa}_1) = C_1 \hat{\kappa}_1^{1/3} \end{equation} }

and

Failed to parse (unknown function "\begin{equation}"): {\displaystyle \begin{equation} \tilde{G}_{22} (\hat{\kappa}_1) = \frac{4}{3} C_1 \hat{\kappa}_1^{1/3} \end{equation} }

You want more? Go to Spectral integration