Decomposing velocity measurements
The quality-controlled velocities can be detrended before being further analysed to determine mean flow past the sensor and surface wave statistics. These quantities are necessary for later choosing the appropriate inertial subrange model for spectral fitting. Quality-controlled velocities may also need detrended before applying various despiking.
Methods for detrending
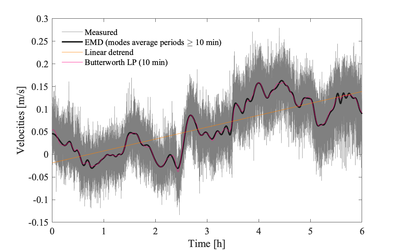
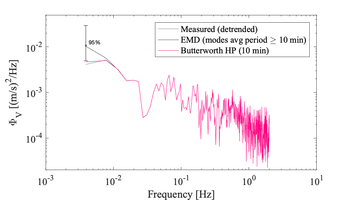
There is no exact definition for what consists of a "trend", nor any set algorithm for identifying the trend. The following techniques can be used for detrending [1]:
- Linear trend removal
- Low-pass linear filters
- Empirical modal decomposition
The first two methods presume the original time series is stationary and linear, while the third is adaptive and applicable to nonlinear and non-stationary timeseries.
Application to measured velocities
Measurements are typically collected in the following two ways:
- continuously, or in such long bursts that they can be considered continuous
- short bursts that are typically at most 2-3x the expected largest turbulence time scales.
As a rule of thumb, turbulence estimates from the inertial subrange of velocity rely on 5 to 15 min long segments.
Segmenting
The act of chopping a timeseries into smaller subsets, i.e., segments, is effectively a form of low-pass (box-car) filtering. The question of how to detrend becomes less important than how best to segment the timeseries. This segmenting step dictates the minimum burst duration when setting-up your equipment.
-
Zoom of the first 512 s of the measured velocities shown above -
Example velocity spectra of the short 512 s of records before and after different detrending techniques applied to the original 6h time series
Notes
- ↑ Jump up to: 1.0 1.1 Zhaohua Wu, Norden E. Huang, Steven R. Long and and Chung-Kang Peng. 2007. On the trend, detrending, and variability of nonlinear and nonstationary time series. PNAS. doi:10.1073/pnas.0701020104
