Segmenting datasets

Once the raw observations have been quality-controlled, then you must split the time series into shorter segments by considering:

• Time and length scales of turbulence
• Stationarity of the segment and Taylor's frozen turbulence hypothesis
• Statistical significance of the resulting spectra

Measured velocities at 4 Hz from an Acoustic-Doppler Velocimeters have been detrended using three different techniques. Empirical modal decomposition (EMD) , linear trend, and a 2nd order low-pass Butterworth filter. A cut-off period of 10 min was targeted by both the filter and EMD

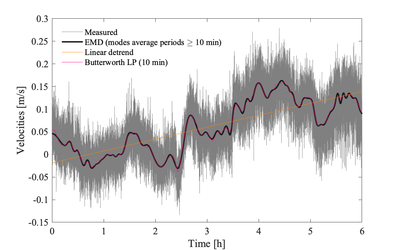
Application to measured velocities

Measurements are typically collected in the following two ways:

• continuously, or in such long bursts that they can be considered continuous
• short bursts that are typically at most 2-3x the expected largest turbulence time scales (e.g., 10 min in ocean environments)

This segmenting step dictates the minimum burst duration when setting up your equipment. The act of chopping a time series into smaller subsets, i.e., segments, is effectively a form of low-pass (box-car) filtering. How to segment the time series is usually a more important consideration than detrending the time series since estimating <math>\varepsilon</math> relies on resolving the inertial subrange in the final spectra computed over each segment.

• 

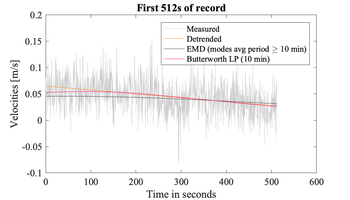
  Zoom of the first 512 s segment of the measured velocities shown above including the same trends

• 

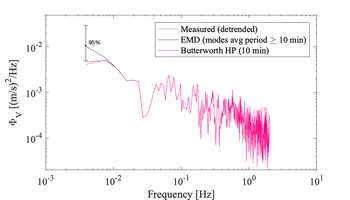
  Example velocity spectra of the short 512 s of records before and after different detrending techniques applied to the original 6h time series. The impact of the detrending method can be seen at the lowest frequencies only

Trade-offs when choosing segment length

The shorter the segment, the higher the temporal resolution of the final <math>\varepsilon</math> time series.