Segmenting datasets: Difference between revisions
mNo edit summary |
mNo edit summary |
||
| Line 3: | Line 3: | ||
* [[Stationarity]] of the segment and [[Taylor's Frozen Turbulence| Taylor's frozen turbulence hypothesis]] | * [[Stationarity]] of the segment and [[Taylor's Frozen Turbulence| Taylor's frozen turbulence hypothesis]] | ||
* Statistical significance of the resulting spectra | * Statistical significance of the resulting spectra | ||
[[File:Long timeseries.png|400px|thumb|Measured velocities at 4 Hz from an [[Acoustic-Doppler Velocimeters]] have been detrended using three different techniques. Empirical modal decomposition (EMD) <ref name="Wuetal_PNAS">{{Cite journal | [[File:Long timeseries.png|400px|thumb|Measured velocities at 4 Hz from an [[Acoustic-Doppler Velocimeters]] have been detrended using three different techniques. Empirical modal decomposition (EMD) <ref name="Wuetal_PNAS">{{Cite journal | ||
| Line 15: | Line 11: | ||
|doi=10.1073/pnas.0701020104 | |doi=10.1073/pnas.0701020104 | ||
}}</ref>, linear trend, and a 2nd order low-pass Butterworth filter. A cut-off period of 10 min was targeted by both the filter and EMD]] | }}</ref>, linear trend, and a 2nd order low-pass Butterworth filter. A cut-off period of 10 min was targeted by both the filter and EMD]] | ||
The shorter the segment, the higher the temporal resolution of the final <math>\varepsilon</math> time series and the more likely the segment will be [[Stationarity|stationary]]. However, the spectrum's lowest resolved frequency and frequency resolution depends on the duration of the signal used to construct the spectrum. Therefore, the segment must remain sufficiently long such that the lowest wavenumber (frequencies) of the [[Velocity inertial subrange|inertial subrange]] are resolved by the spectra. This is particularly important when measurement noise drowns the highest wavenumber (frequencies) of the inertial subrange. Thus, using too short segments may inadvertently render the resulting spectra unusable for deriving <math>\varepsilon</math> from the [[Velocity inertial subrange|inertial subrange]]. | |||
==Application to measured velocities== | ==Application to measured velocities== | ||
Revision as of 15:35, 30 November 2021
Once the raw observations have been quality-controlled, then you must split the time series into shorter segments by considering:
- Time and length scales of turbulence
- Stationarity of the segment and Taylor's frozen turbulence hypothesis
- Statistical significance of the resulting spectra
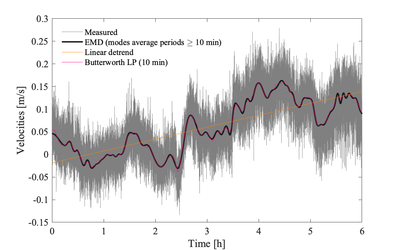
The shorter the segment, the higher the temporal resolution of the final <math>\varepsilon</math> time series and the more likely the segment will be stationary. However, the spectrum's lowest resolved frequency and frequency resolution depends on the duration of the signal used to construct the spectrum. Therefore, the segment must remain sufficiently long such that the lowest wavenumber (frequencies) of the inertial subrange are resolved by the spectra. This is particularly important when measurement noise drowns the highest wavenumber (frequencies) of the inertial subrange. Thus, using too short segments may inadvertently render the resulting spectra unusable for deriving <math>\varepsilon</math> from the inertial subrange.
Application to measured velocities
Measurements are typically collected in the following two ways:
- continuously, or in such long bursts that they can be considered continuous
- short bursts that are typically at most 2-3x the expected largest turbulence time scales (e.g., 10 min in ocean environments)
This segmenting step dictates the minimum burst duration when setting up your equipment. The act of chopping a time series into smaller subsets, i.e., segments, is effectively a form of low-pass (box-car) filtering. How to segment the time series is usually a more important consideration than detrending the time series since estimating <math>\varepsilon</math> relies on resolving the inertial subrange in the final spectra computed over each segment.
-
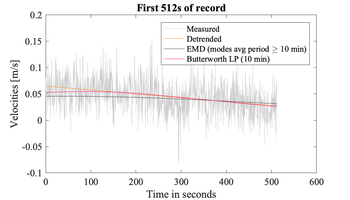
Zoom of the first 512 s segment of the measured velocities shown above including the same trends -
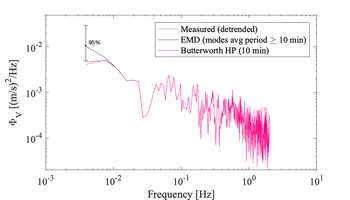
Example velocity spectra of the short 512 s of records before and after different detrending techniques applied to the original 6h time series. The impact of the detrending method can be seen at the lowest frequencies only
Notes
- ↑ {{#arraymap:Zhaohua Wu, Norden E. Huang, Steven R. Long, and Chung-Kang Peng|,|x|x|, |and}}. 2007. On the trend, detrending, and variability of nonlinear and nonstationary time series. PNAS. doi:10.1073/pnas.0701020104
