Segmenting datasets: Difference between revisions
| Line 27: | Line 27: | ||
{{FontColor|fg=white|bg=red|text= include example data in plot highlighting low and high epsilon, and different speeds leading to much shorter and longer segmenting periods}} | {{FontColor|fg=white|bg=red|text= include example data in plot highlighting low and high epsilon, and different speeds leading to much shorter and longer segmenting periods}} | ||
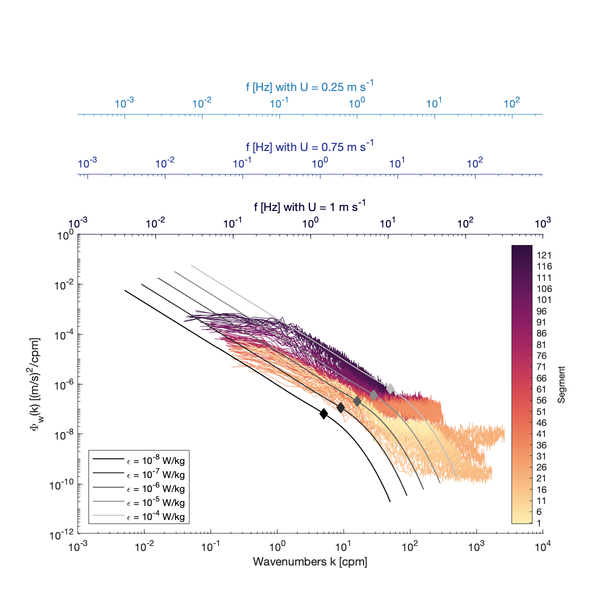
[[File:Segment_anisotropy.png|center|thumbnail|600px|Example theoretical velocity spectra for different <math>\varepsilon</math> with the empirical limit <math>\hat{k}L_k\sim0.1</math> denoted by the diamonds (<math>\hat{k}</math> is in rad/m). The inertial subrange extends to smaller wavenumber <math>k</math> [cpm] as <math>\varepsilon</math> increases. The lowest frequency resolved by a spectra depends on the fft-length used when computing the spectra. The colored lines are spectral observations from a dataset with fast speeds and large <math>\varepsilon</math>, allowing the use of relatively short segments (128s) to estimate the spectra from fft-length of 32 s (2048 samples @ 64 Hz)]] | [[File:Segment_anisotropy.png|center|thumbnail|600px|Example theoretical velocity spectra for different <math>\varepsilon</math> with the empirical limit <math>\hat{k}L_k\sim0.1</math> denoted by the diamonds (<math>\hat{k}</math> is in rad/m). The inertial subrange extends to smaller wavenumber <math>k</math> [cpm] as <math>\varepsilon</math> increases. The lowest frequency resolved by a spectra depends on the fft-length used when computing the spectra. The colored lines are spectral observations from a dataset with fast speeds and large <math>\varepsilon</math>, allowing the use of relatively short segments (128s) to estimate the spectra from fft-length of 32 s (2048 samples @ 64 Hz). The impact of [[Velocity inertial subrange model#anisotropy|turbulence anisotropy]] is also visible through the flattening of the spectra around 1 cpm]] | ||
==Notes== | ==Notes== | ||
Revision as of 17:30, 5 July 2022
Once the raw observations have been quality-controlled, then you must split the time series into shorter segments by considering:
- Time and length scales of turbulence
- Stationarity of the segment and Taylor's frozen turbulence hypothesis
- Statistical significance of the resulting spectra
Considerations
Measurements are typically collected in the following two ways:
- continuously, or in such long bursts that they can be considered continuous
- short bursts that are typically at most 2-3x the expected largest turbulence time scales (e.g., 10 min in ocean environments)
This segmenting step dictates the minimum burst duration when setting up your equipment. The act of chopping a time series into smaller subsets, i.e., segments, is effectively a form of low-pass (box-car) filtering. How to segment the time series is usually a more important consideration than detrending the time series since estimating
-
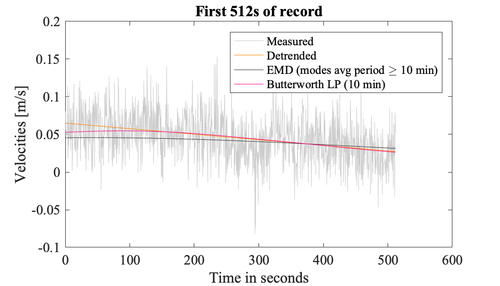
512 s segment of the measured velocities after applying different detrending methods -
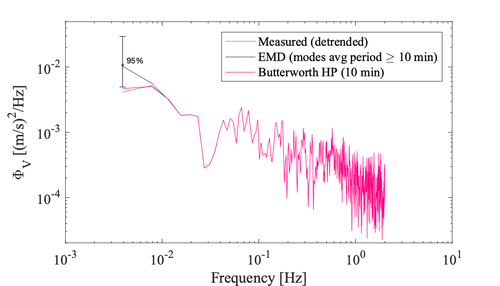
Example velocity spectra of the short 512 s of records before and after different detrending techniques applied to the original 6h time series. The impact of the detrending method can be seen at the lowest frequencies only
Trade-offs
The shorter the segment, the higher the temporal resolution of the final
Recommendations
A good rule of thumb for tidally-influenced environments is 5 to 15 min segments, but this may be shorter in certain energetic and fast-moving flows. include example data in plot highlighting low and high epsilon, and different speeds leading to much shorter and longer segmenting periods
Notes
Return to Preparing_quality-controlled_velocities
