Segmenting datasets: Difference between revisions
From Atomix
m Becoming segmenting only page |
m added links to old images |
||
| Line 1: | Line 1: | ||
Once the raw | Once the raw observations have been [[Data processing of raw measurements|quality-controlled]], then you must split the time series into shorter segments by considering: | ||
** time and length scales of turbulence | ** time and length scales of turbulence | ||
** [[Stationarity|stationarity]] of the segment | ** [[Stationarity|stationarity]] of the segment | ||
** [[Taylor's Frozen Turbulence| Taylor's frozen turbulence hypothesis]], etc ... | ** [[Taylor's Frozen Turbulence| Taylor's frozen turbulence hypothesis]], etc ... | ||
[[File:Long timeseries.png|400px|thumb|Measured velocities at 4 Hz from an [[Acoustic-Doppler Velocimeters]] have been detrended using three different techniques. Empirical modal decomposition (EMD) <ref name="Wuetal_PNAS">{{Cite journal | |||
|authors=Zhaohua Wu, Norden E. Huang, Steven R. Long, and Chung-Kang Peng | |||
|journal_or_publisher=PNAS | |||
|paper_or_booktitle=On the trend, detrending, and variability of nonlinear and nonstationary time series | |||
|year=2007 | |||
|doi=10.1073/pnas.0701020104 | |||
}}</ref>, linear trend, and a 2nd order low-pass Butterworth filter. A cut-off period of 10 min was targeted by both the filter and EMD]] | |||
==Application to measured velocities== | |||
Measurements are typically collected in the following two ways: | |||
* continuously, or in such long bursts that they can be considered continuous | |||
* short bursts that are typically at most 2-3x the expected largest [[Time and length scales of turbulence|turbulence time scales]] (e.g., 10 min in ocean environments) | |||
The act of chopping a time series into smaller subsets, i.e., segments, is effectively a form of low-pass (box-car) filtering. Hence, when estimating <math>\varepsilon</math> how to [[Segmenting datasets|segment]] the time series is usually a more important consideration than [[Detrending time series|detrending time series]]. This segmenting step dictates the minimum burst duration when setting-up your equipment. | The act of chopping a time series into smaller subsets, i.e., segments, is effectively a form of low-pass (box-car) filtering. Hence, when estimating <math>\varepsilon</math> how to [[Segmenting datasets|segment]] the time series is usually a more important consideration than [[Detrending time series|detrending time series]]. This segmenting step dictates the minimum burst duration when setting-up your equipment. | ||
| Line 16: | Line 26: | ||
==Notes== | |||
<references/> | |||
[[Category:Velocity point-measurements]] | [[Category:Velocity point-measurements]] | ||
Revision as of 14:24, 30 November 2021
Once the raw observations have been quality-controlled, then you must split the time series into shorter segments by considering:
- time and length scales of turbulence
- stationarity of the segment
- Taylor's frozen turbulence hypothesis, etc ...
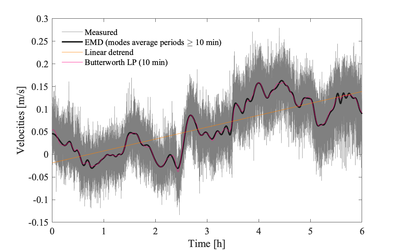
Application to measured velocities
Measurements are typically collected in the following two ways:
- continuously, or in such long bursts that they can be considered continuous
- short bursts that are typically at most 2-3x the expected largest turbulence time scales (e.g., 10 min in ocean environments)
The act of chopping a time series into smaller subsets, i.e., segments, is effectively a form of low-pass (box-car) filtering. Hence, when estimating [math]\displaystyle{ \varepsilon }[/math] how to segment the time series is usually a more important consideration than detrending time series. This segmenting step dictates the minimum burst duration when setting-up your equipment.
-

Zoom of the first 512 s of the measured velocities shown above including the same trends -
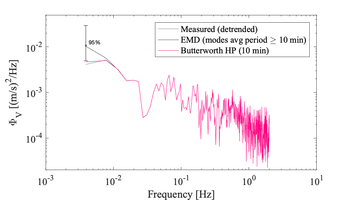
Example velocity spectra of the short 512 s of records before and after different detrending techniques applied to the original 6h time series. The impact of the detrending method can be seen at the lowest frequencies only
Notes
- ↑ Zhaohua Wu, Norden E. Huang, Steven R. Long and and Chung-Kang Peng. 2007. On the trend, detrending, and variability of nonlinear and nonstationary time series. PNAS. doi:10.1073/pnas.0701020104
