Segmenting datasets
Once the raw observations have been quality-controlled, then you must split the time series into shorter segments by considering:
- Time and length scales of turbulence
- Stationarity of the segment and Taylor's frozen turbulence hypothesis
- Required statistical significance of the resulting spectra (only important if you need to remove motion-induced contamination from the spectra)
Considerations
Measurements are typically collected in the following two ways:
- continuously, or in such long bursts that they can be considered continuous
- short bursts that are typically at most 2-3x the expected largest turbulence time scales (e.g., 10 min in ocean environments)
This segmenting step dictates the minimum burst duration when setting up your equipment. The act of chopping a time series into smaller subsets, i.e., segments, is effectively a form of low-pass (box-car) filtering. The length of the segment in time is usually a more important consideration than detrending the time series when estimating [math]\displaystyle{ \varepsilon }[/math] from the inertial subrange of the final spectra.
The shorter the segment, the higher the temporal resolution of the final [math]\displaystyle{ \varepsilon }[/math] time series, and the more likely the segment will be stationary. The segment must remain sufficiently long such that the lowest wavenumber (frequencies) of the inertial subrange are retained by the spectra. This is particularly important when measurement noise drowns the highest wavenumber (frequencies) of the inertial subrange. Thus, using too short segments may inadvertently render the spectra unusable for deriving [math]\displaystyle{ \varepsilon }[/math] from the inertial subrange by virtue of no longer resolving this subrange as shown in (Fig. 3).
Spectral estimation
The spectrum's lowest resolved frequency and final resolution are the inverse of the fft-length, i.e., the duration of the signal used to construct the spectrum. The spectra are often estimated by block averaging numerous spectra (FFT) estimated from smaller chunks of data within each segment. Another strategy is band-averaging spectra in the frequency domain. The fft-length i.e., the duration of data used to estimate each spectrum, is thus an important quantity that dictates the final range of frequencies resolved by the spectra.
Recommendations
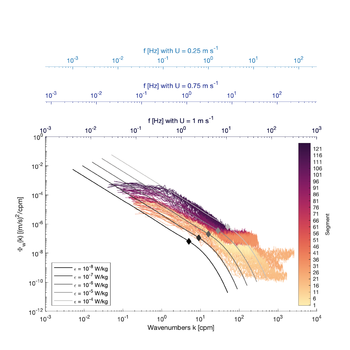
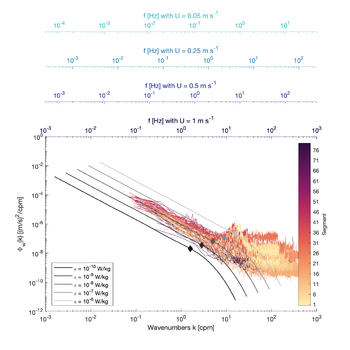
A good rule of thumb for tidally-influenced environments is 5 to 15 min segments, but this may be shorter in certain energetic and fast-moving flows (Fig. 1) and longer in less energetic environments (Fig.2).
Fig. 3 provides a guide to the fft-length required for resolving different subrange as a function of the speed past the sensor, and [math]\displaystyle{ \varepsilon }[/math]. For instance, an fft-length of 4 s would resolve one decade of the inertial subrange at speeds past the sensor of 0.5 m/s and [math]\displaystyle{ \varepsilon\sim10^{-7} }[/math] W/kg. Longer segments would be required for slower flows or lower [math]\displaystyle{ \varepsilon }[/math]. At [math]\displaystyle{ \varepsilon\approx10^{-9} }[/math] W/kg, one decade of the inertial subrange would be resolved with an fft-length longer than 10s provided the speed was faster than 0.5 m/s.
Because the inertial subrange may be contaminated at the highest wavenumbers by instrument noise, we suggest using longer segments than the minimum. This strategy also enables having a larger number of spectral observations to fit over the inertial subrange given the spectral resolution also depends on the fft-length.
The final segment length may be larger than the fft-length if using block averaging for the spectral computations. Is this explained in the spectral page?
Are the peaks in the MAVS data vortex shedding from the rings. Check the motion sensors onboard?
Return to Preparing_quality-controlled_velocities
